Skip to main content

Теория: Кусочно-линейная функция. Горизонтальная прямая

Задание

Постройте график функции

\(\displaystyle y=\begin{cases}4x-5, \,\,\small{если}\,\,\, x<1,\\-2{,}5x+5, \,\,\small{если}\,\,\, 1\leqslant x \leqslant 4,\\x-9, \,\,\small{если}\,\,\, x>4.\end{cases}\)

Определите, при каких значениях \(\displaystyle m\) прямая \(\displaystyle y=m\) имеет с графиком ровно две общие точки.

Выберите верный ответ:

Решение

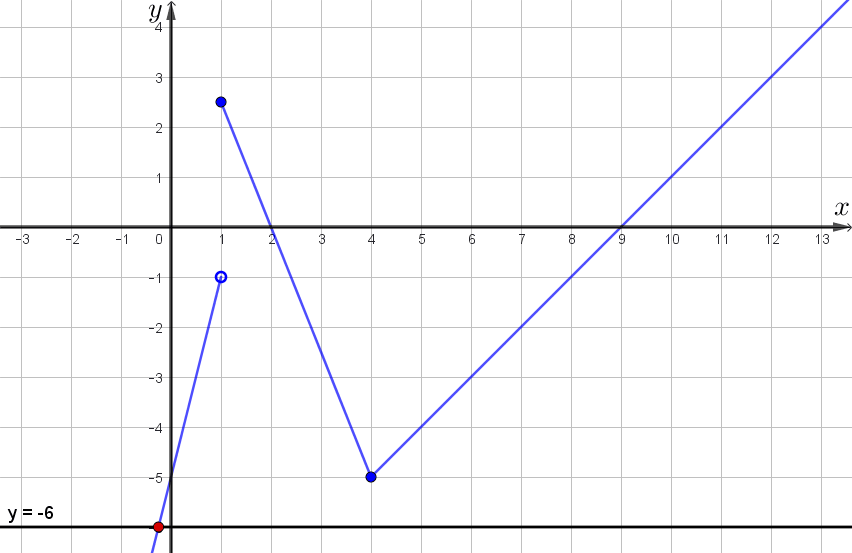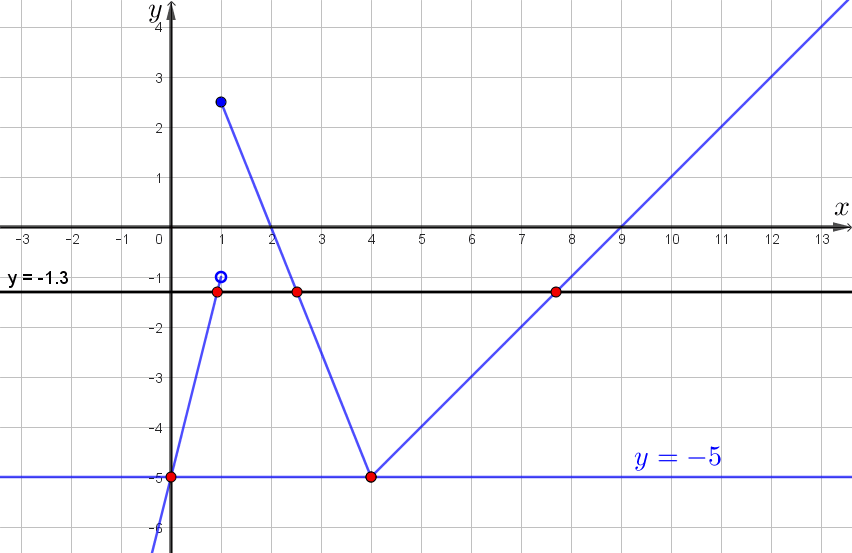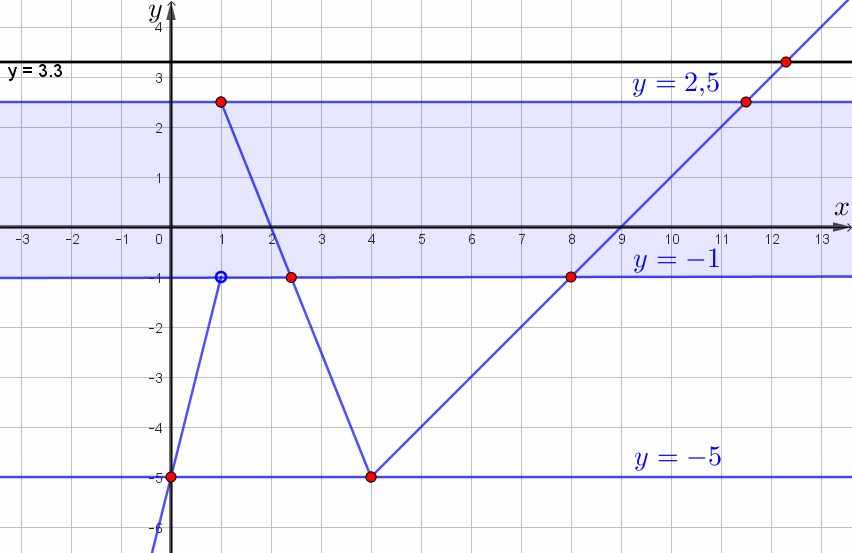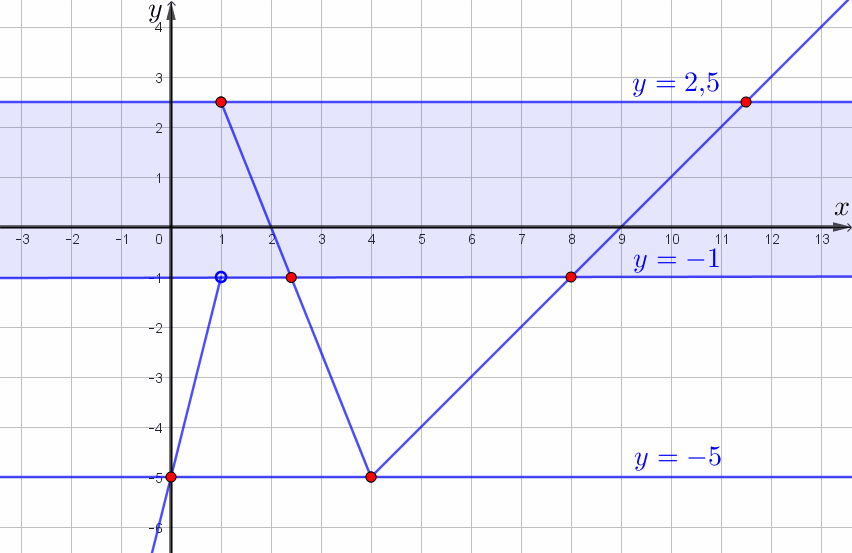
Построим график кусочно-заданной функции по шагам:

  • сначала построим график \(\displaystyle y=4x-5 \) для \(\displaystyle x<1,\)
  • затем  построим график \(\displaystyle y=-2{,}5x+5 \) для \(\displaystyle 1\leqslant x\leqslant 4\)
  • и построим график \(\displaystyle y=x-9\) для \(\displaystyle x>4\small.\)

Строим график \(\displaystyle y=4x-5 \) для \(\displaystyle x<1\small.\)

Строим график \(\displaystyle y=-2{,}5x+5 \) для \(\displaystyle 1\leqslant x\leqslant 4\small.\)

Строим график \(\displaystyle y=x-9\) для \(\displaystyle x>4\small.\)

Объединяя, получаем график кусочно-заданной функции.

\(\displaystyle y= \begin{cases} 4x-5, \,\,\small{если}\,\,\, x<1,\\ -2{,}5x+5, \,\,\small{если}\,\,\, 1\leqslant x \leqslant 4,\\ x-9, \,\,\small{если}\,\,\, x>4. \end{cases} \)


Запишем координаты граничных точек:

 \(\displaystyle x=1\)\(\displaystyle x=4\)
\(\displaystyle y=4x-5\)\(\displaystyle -1\) 
\(\displaystyle y=-2{,}5x+5\)\(\displaystyle 2{,}5\)\(\displaystyle -5\)
\(\displaystyle y=x-9\) \(\displaystyle -5\)

 

Определим, при каких значениях \(\displaystyle y=m\) пересекает график ровно в двух точках.

Прямая \(\displaystyle y=m\) – горизонтальная прямая.

Меняя значение \(\displaystyle m,\) будем двигать данную прямую.

Определим, когда она имеет с графиком ровно две общие точки:

Таким образом, прямая \(\displaystyle y=m\) имеет с графиком ровно две общие точки при

\(\displaystyle m\in\{-5\}\cup[-1;\, 2{,}5]\small.\)

Ответ: \(\displaystyle m\in\{-5\}\cup[-1;\, 2{,}5]\small.\)