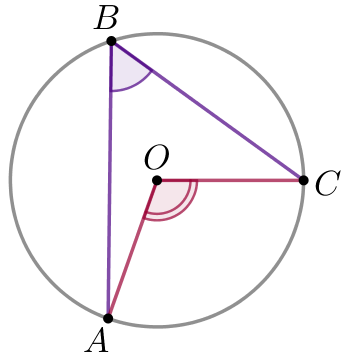
Радиус окружности равен \(\displaystyle 2 \small.\) Найдите величину острого вписанного угла, опирающегося на хорду длины \(\displaystyle 2\sqrt{3} \small.\) Ответ дайте в градусах.
Пусть \(\displaystyle O\) – центр окружности, \(\displaystyle OA=OC=2\) – ее радиусы, \(\displaystyle AC=2\sqrt{3}\) – данная по условию хорда, \(\displaystyle \angle ABC\) – вписанный острый угол, опирающийся на хорду \(\displaystyle AC \small.\)
В задаче требуется найти \(\displaystyle \angle ABC \small.\)
Рассмотрим треугольник \(\displaystyle OAC \small.\)
Треугольник \(\displaystyle OAC\) равнобедренный, так как \(\displaystyle OA=OC \small.\)
Проведем высоту \(\displaystyle OH\) треугольника \(\displaystyle OAC \small.\)
Так как высота \(\displaystyle OH\) равнобедренного треугольника \(\displaystyle AOC \small,\) опущенная на основание, является и медианой, то
\(\displaystyle CH=\frac{1}{2}\cdot AC=\frac{1}{2} \cdot 2\sqrt {3}=\sqrt{3} \small.\)
Рассмотрим треугольник \(\displaystyle OCH \small.\)
В треугольнике \(\displaystyle OCH \small: \)
По теореме Пифагора \(\displaystyle OC^2=OH^2+CH^2\small.\) Значит, \(\displaystyle OH^2=OC^2-CH^2 \small,\) \(\displaystyle OH^2=2^2-(\sqrt{3})^2=4-3=1=1^2\small.\) |
Поскольку длина отрезка положительна, то \(\displaystyle OH=1\small.\)
В прямоугольном треугольнике \(\displaystyle OCH\) катет, лежащий против угла \(\displaystyle OCH \small,\) равен половине гипотенузы. Значит,
\(\displaystyle \angle OCH =30^{\circ}\small .\)
Так как сумма углов треугольника \(\displaystyle OCH\) равна \(\displaystyle 180^{\circ}\small ,\) то
\(\displaystyle \angle COH =180^{\circ} - \angle OCH -\angle OHC =180^{\circ}-30^{\circ}-90^{\circ}=60^{\circ}\small .\)
Поскольку высота равнобедренного треугольника, опущенная на основание, является также и биссектрисой, то
\(\displaystyle \angle AOC =2 \cdot \angle COH =2\cdot 60^{\circ}=120^{\circ}\small .\)
Угол \(\displaystyle AOC \) центральный, опирающийся на ту же дугу, что и вписанный угол \(\displaystyle ABC \small.\)
Так как \(\displaystyle \angle ABC\) острый, то \(\displaystyle \angle ABC < 90^{\circ} {\small ,}\) и по правилу
Связь величин вписанного и центрального углов
|
|
| 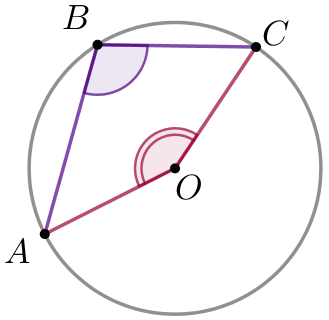 |
\(\displaystyle \angle AOC =2 \cdot \angle ABC{\small .} \)
Следовательно,
\(\displaystyle \angle ABC =\frac{1}{2}\cdot \angle AOC=\frac{1}{2}\cdot 120^{\circ}= 60^{\circ}{\small .} \)
Ответ: \(\displaystyle 60 {\small .}\)