Skip to main content

Теория: 19 Радиусы и хорды

Задание

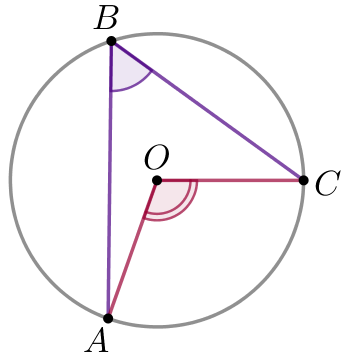
Найдите хорду, на которую опирается угол \(\displaystyle 150^\circ \small,\) вписанный в окружность радиуса \(\displaystyle 3 \small.\)

Решение

Проведем радиусы \(\displaystyle OA\) и \(\displaystyle OC\) окружности, \(\displaystyle OA=OC=3 \small,\) \(\displaystyle AOC \) – центральный угол.

Так как \(\displaystyle \angle ABC=150^{\circ} > 90^{\circ} {\small ,}\) то по правилу

Правило

Связь величин вписанного и центрального углов

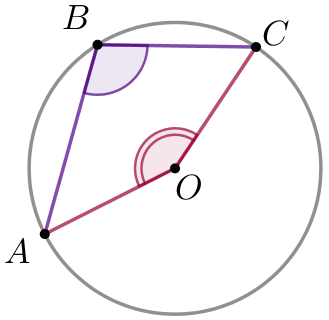  • \(\displaystyle \angle AOC =2 \cdot \angle ABC \small, \) если \(\displaystyle \angle ABC\leqslant 90^{\circ} \small,\)

  • \(\displaystyle \angle AOC =2 \cdot (180^{\circ}-\angle ABC) \small, \) если \(\displaystyle \angle ABC>90^{\circ} \small.\)

получаем:

\(\displaystyle \angle AOC =2 \cdot (180^{\circ}-\angle ABC){\small .} \)

Значит, 

\(\displaystyle \angle AOC =2 \cdot (180^{\circ}- 150^{\circ})=2\cdot 30 ^{\circ}= 60^{\circ} \small.\)

Рассмотрим равнобедренный треугольник \(\displaystyle OAC \small.\)

По свойству равнобедренного треугольника углы при основании \(\displaystyle AC\) равны.

Поскольку сумма углов треугольника равна \(\displaystyle 180^{\circ}{\small ,} \) то

\(\displaystyle \angle OAC =\angle OCA = \frac{180^{\circ}-60^{\circ}}{2}=60^{\circ} \small.\)

Так как все углы треугольника \(\displaystyle OAC\) составляют \(\displaystyle 60^{\circ} \small,\) то треугольник \(\displaystyle AOC\) – равносторонний.

Следовательно, 

\(\displaystyle AC=OA=OC=3 \small.\)

Ответ: \(\displaystyle 3 {\small .}\)