Задание
Площадь ромба равна \(\displaystyle 6 \small.\) Одна из его диагоналей на \(\displaystyle 1\) больше другой. Найдите меньшую диагональ.
Решение
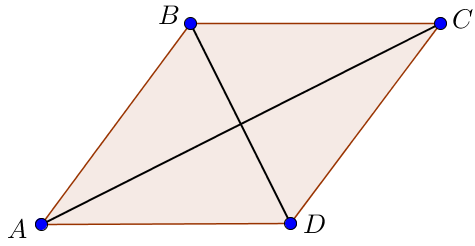
Пусть \(\displaystyle BD=x\) – меньшая диагональ ромба, тогда \(\displaystyle AC=x+1 \) – большая диагональ ромба.
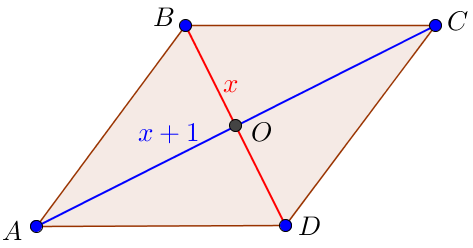
Поскольку площадь ромба равна половине произведения диагоналей
\(\displaystyle S=\frac{1}{2} AC\cdot BD \small,\)
то
\(\displaystyle 6 = \frac{1}{2} \cdot (x+1)\cdot x {\small .}\)
Получаем:
\(\displaystyle 12 = (x+1) \cdot x {\small,}\)
\(\displaystyle x^2+x-12=0 \small.\)
Решим квадратное уравнение.
\(\displaystyle x_1=3\) и \(\displaystyle x_2=-4\) корни уравнения \(\displaystyle x^2+x-12=0\)
Так как длина отрезка положительна, то \(\displaystyle x=3 \small.\) Следовательно, длина меньшей диагонали ромба равна \(\displaystyle 3 \small.\)
Ответ: \(\displaystyle 3{\small .}\)