Треугольник \(\displaystyle ABC\) вписан в окружность с центром \(\displaystyle O \small,\) причем \(\displaystyle AC=4 \small,\) \(\displaystyle \sin \angle B=0{,}4\)(см.рис.). Найдите диаметр окружности.
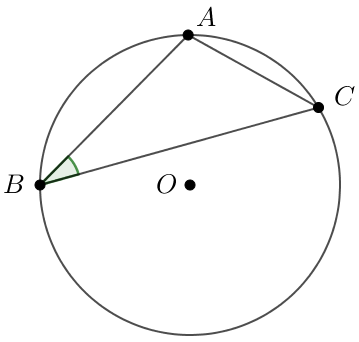
Построим диаметр \(\displaystyle AD \) и соединим отрезком точки \(\displaystyle D\) и \(\displaystyle C \small. \)
Вписанные углы \(\displaystyle ABC\) и \(\displaystyle ADC\) опираются на одну дугу, а значит равны. Тогда
\(\displaystyle \sin \angle D=\sin \angle B=0{,}4 \small.\)
Поскольку вписанный угол, опирающийся на диаметр, равен \(\displaystyle 90^ {\circ}\), то треугольник \(\displaystyle ADC\) прямоугольный.
В прямоугольном треугольнике \(\displaystyle ADC\)
\(\displaystyle \sin \angle D=\frac{AC}{AD} \small.\)
Тогда
\(\displaystyle AD=\frac{AC}{\sin \angle D}=\frac{4}{0{,}4}=10 \small.\)
Следовательно, диаметр окружности равен \(\displaystyle 10 \small.\)
Ответ: \(\displaystyle 10 {\small .}\)
Изучение связи между острым углом \(\displaystyle ABC \small,\) стороной \(\displaystyle AC\) и диаметром описанной окружности позволяет получить следующее соотношение:
Связь между стороной треугольника, противоположным углом и радиусом описанной окружности
Если в треугольнике \(\displaystyle ABC\) угол \(\displaystyle ABC\) острый, то
\(\displaystyle \frac{AC}{\sin \angle B}=2R,\)
где \(\displaystyle R\) – радиус описанной окружности.