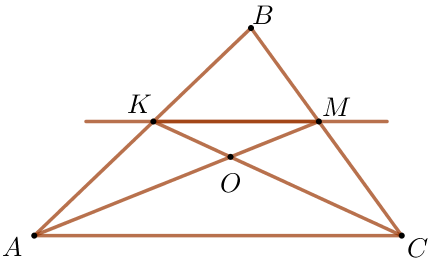
Прямая, параллельная стороне \(\displaystyle AC\) треугольника \(\displaystyle ABC{\small,}\) пересекает стороны \(\displaystyle AB\) и \(\displaystyle BC\) в точках \(\displaystyle K\) и \(\displaystyle M\) соответственно. Отрезки \(\displaystyle AM\) и \(\displaystyle CK\) пересекаются в точке \(\displaystyle O {\small.}\) Найдите \(\displaystyle BK {\small,}\) если \(\displaystyle OM:AO=3:7 {\small,}\) \(\displaystyle AB=14 {\small.}\)
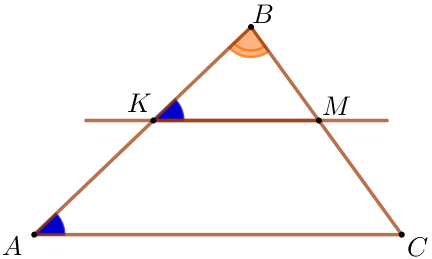
Так как \(\displaystyle KM \parallel AC {\small,} \) \(\displaystyle AB\) – секущая, то \(\displaystyle \angle BKM= \angle BAC\) \(\displaystyle (\)соответственные углы\(\displaystyle ){\small.}\)
 | Рассмотрим треугольники \(\displaystyle KBM\) и \(\displaystyle ABC {\small:} \\ \)
|
Следовательно,
\(\displaystyle \frac{BK}{BA}= \frac{KM}{AC} {\small,} \\ \)
\(\displaystyle BK= \frac{KM}{AC}\cdot BA {\small.} \\ \)
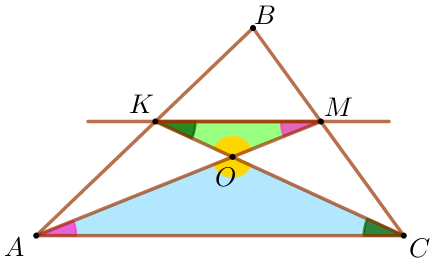 | Рассмотрим треугольники \(\displaystyle KOM\) и \(\displaystyle AOC {\small:}\)
Треугольники \(\displaystyle MOK\) и \(\displaystyle AOC\) подобны по двум углам. |
Следовательно,
\(\displaystyle \frac{KM}{AC}= \frac{OM}{AO} =\frac{3}{7}{\small.} \)
Получаем
\(\displaystyle BK= \frac{KM}{AC}\cdot BA=\frac{3}{7} \cdot 14=6 {\small.} \\ \)
Ответ: \(\displaystyle 6 {\small.}\)