Меньшее из оснований трапеции равно \(\displaystyle 3{\small .}\) Отрезок, соединяющий середины диагоналей трапеции, равен \(\displaystyle 2{\small .}\) Найдите большее основание трапеции.
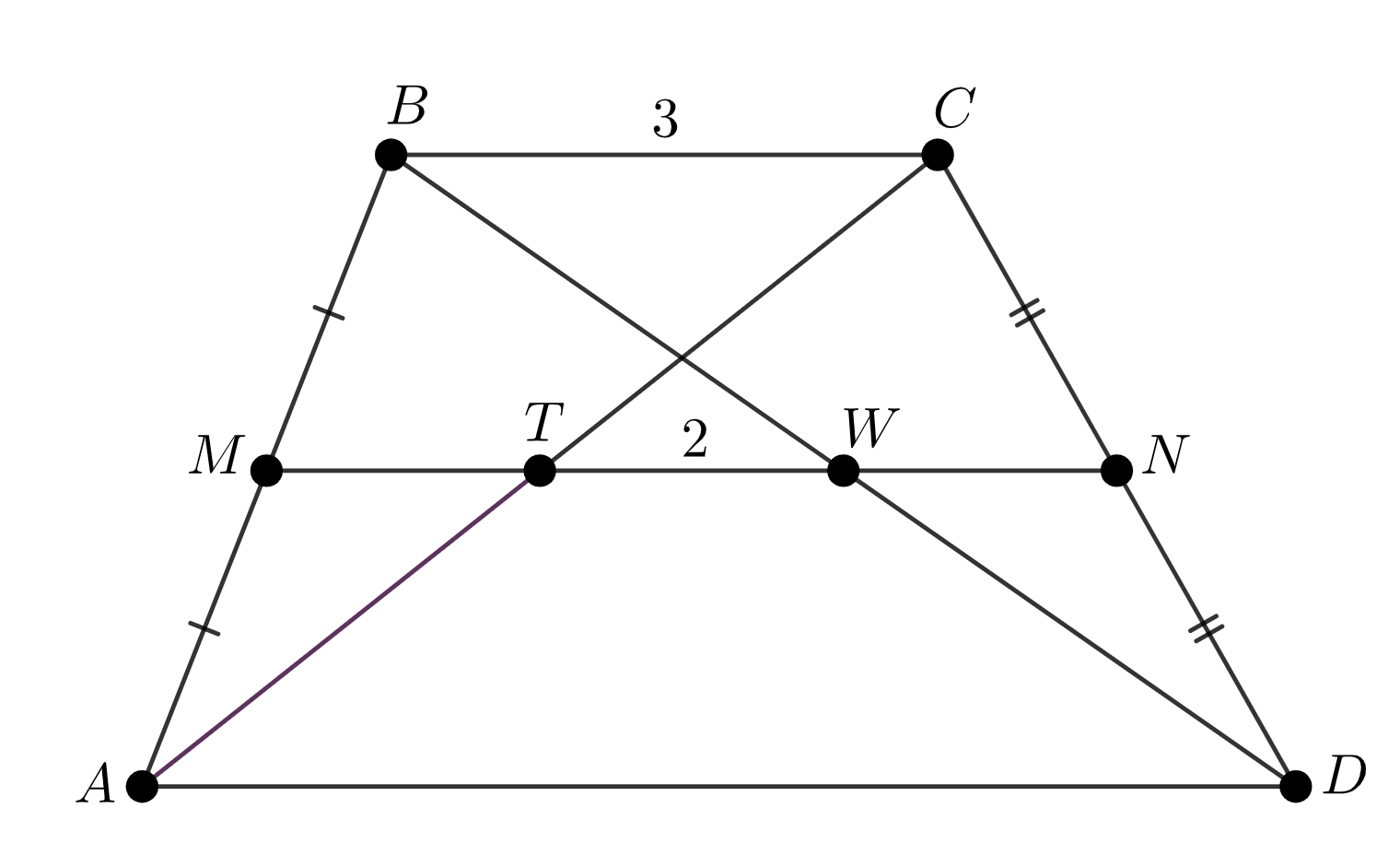
Пусть \(\displaystyle BC=3\) – меньшее основание трапеции \(\displaystyle ABCD{\small ,}\) \(\displaystyle T\) и \(\displaystyle W\) – середины диагоналей
\(\displaystyle AC\) и \(\displaystyle BD\) соответственно, \(\displaystyle TW=2{\small .}\) Требуется найти \(\displaystyle AD{\small .}\)
Пусть \(\displaystyle M\) и \(\displaystyle N\) – середины боковых сторон \(\displaystyle AB\) и \(\displaystyle CD\) соответственно. Проведем среднюю линию \(\displaystyle MN\) трапеции. По свойству средней линии трапеции точки \(\displaystyle T\) и \(\displaystyle W\) лежат на средней линии.
|  |
Поскольку \(\displaystyle MT\) – средняя линия треугольника \(\displaystyle ABC{\small ,}\) то
\(\displaystyle MT=\frac{BC}{2}=\frac{3}{2}{\small .}\)
Так как точка \(\displaystyle T\) лежит на отрезке \(\displaystyle MW{\small ,}\) то
\(\displaystyle MW=MT+TW=\frac{3}{2}+2=\frac{7}{2}{\small .}\)
Но \(\displaystyle MW\) – средняя линия треугольника \(\displaystyle ADB{\small .}\) Значит,
\(\displaystyle MW=\frac{AD}{2}{\small ,}\)
\(\displaystyle AD=2\cdot MW=2\cdot \frac{7}{2}=7{\small .}\)
Ответ: \(\displaystyle 7{\small .}\)