Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна \(\displaystyle 48^\circ\small?\) Ответ дайте в градусах.
Воспользуемся свойством равнобедренной трапеции.
Свойство равнобедренной трапеции
Углы при основании равнобедренной трапеции равны.
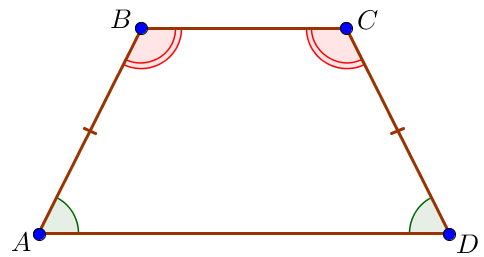
Тогда
\(\displaystyle \color{green}{\angle {ADC}}=\color{green}{\angle {DAB}}\small,\)
\(\displaystyle \color{red}{\angle {ABC}}=\color{red}{\angle {BCD}}\small.\)
Пусть угол \(\displaystyle \color{red}{BCD}\) больше угла \(\displaystyle \color{green}{BAD}\) на \(\displaystyle \color{blue}{48^{\circ}}\small.\) Обозначим \(\displaystyle \color{green}{\angle BAD}=\color{green}{\angle {ADC}}=\color{green}{x}\small,\) тогда \(\displaystyle \color{red}{\angle BCD}=\color{green}{\angle BAD}+\color{blue}{48^{\circ}}=\color{green}{x}+\color{blue}{48}\small.\) Поскольку в трапеции сумма углов при боковой стороне равна \(\displaystyle 180^\circ\small,\) то \(\displaystyle \color{green}{\angle {ADC}}+\angle\color{red}{BCD}= 180^{\circ}\small.\) |
|
Получаем уравнение
\(\displaystyle \color{green}{x}+(\color{red}{x+48})= 180\small,\)
откуда
\(\displaystyle {2x}+48= 180\small,\)
\(\displaystyle {2x} = 132\small,\)
\(\displaystyle {x} = 66\small.\)
Значит, \(\displaystyle \angle BAD={x}=66^{\circ}{ \small } \) и \(\displaystyle {\angle BCD}=x+48=66+48=114^\circ\small.\)
Следовательно, наибольший угол трапеции составляет \(\displaystyle 114^\circ\small.\)
Ответ: \(\displaystyle 114 \small.\)
