В равнобедренной трапеции с меньшим основанием \(\displaystyle 23\) и высотой \(\displaystyle 39\) тангенс острого угла равен \(\displaystyle \frac{13}{8} \small.\) Найдите большее основание трапеции.
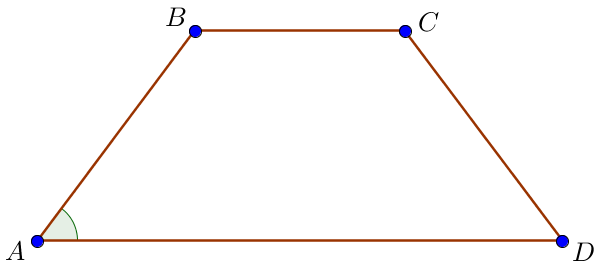
Пусть \(\displaystyle BC=23\) – меньшее основание, \(\displaystyle AB=CD\) – боковые стороны равнобедренной трапеции \(\displaystyle ABCD \small.\) По свойству равнобедренной трапеции углы при основании равны, \(\displaystyle \tg \angle A=\tg \angle D=\frac{13}{8} \small.\) Требуется найти основание \(\displaystyle AD \small.\) Проведем высоты \(\displaystyle BH = CK =39 \) трапеции. |  |
Отрезок \(\displaystyle AH \) найдем из треугольника \(\displaystyle ABH \small.\) Нам известны \(\displaystyle \tg \angle BAH=\frac{13}{8}\) и противолежащий острому углу \(\displaystyle BAH\) катет \(\displaystyle BH=39 \small.\) Так как \(\displaystyle \tg \angle BAH=\frac{BH}{AH} \small,\) то \(\displaystyle AH=\frac{BH}{\tg \angle BAH}=\frac{39}{\phantom{1}{\displaystyle\frac{13}{8}}\phantom{1}}=\frac{39\cdot 8}{13}=3\cdot 8=24 \small.\) | 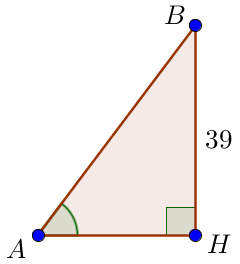 |
Поскольку основания трапеции параллельны, а высоты трапеции перпендикулярны основаниям, \(\displaystyle BH K C \) – прямоугольник. Тогда \(\displaystyle H K =BC=23 \small.\)
Прямоугольные треугольники \(\displaystyle ABH\) и \(\displaystyle DCK\) равны по гипотенузе \(\displaystyle AB=CD\) и катету \(\displaystyle BH=CK \small.\) Значит, \(\displaystyle DK=AH=24\) и \(\displaystyle AD=AH+HK+DK=\) \(\displaystyle =24+23+24=71 \small.\) |  |
Ответ: \(\displaystyle 71 \small.\)