В параллелограмме \(\displaystyle ABCD\) известны длины сторон \(\displaystyle AB=3 \small,\) \(\displaystyle AD=21\small\) и \(\displaystyle \sin \angle A=\frac{6}{7} \small.\) Найдите большую высоту параллелограмма.
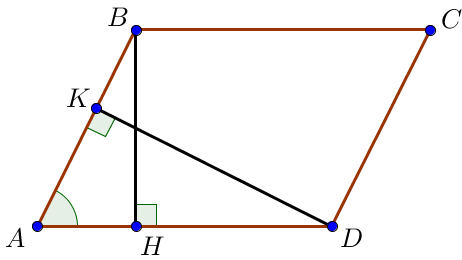
Первый способ решения
Площадь параллелограмма может быть найдена как произведение смежных сторон на синус угла между ними:
\(\displaystyle {S_{пар}} = {AB}\cdot AD \cdot \sin \angle A = {3}\cdot 21\cdot \frac{6}{7} = 3 \cdot 3\cdot 6=54 {\small.}\)
Площадь параллелограмма может быть также найдена как произведение основания на высоту. С одной стороны,
\(\displaystyle {S_{пар}} = {AD}\cdot BH {\small.}\)
\(\displaystyle {54} = {21}\cdot BH {\small,}\)
откуда
\(\displaystyle BH=\frac{54}{21}=\frac{18}{7} {\small . }\)
С другой стороны,
\(\displaystyle {S_{пар}} = {AB}\cdot DK {\small}\)
\(\displaystyle {54} = {3}\cdot DK {\small,}\)
откуда
\(\displaystyle DK=\frac{54}{3}={18}{\small . }\)
Тогда большая высота равна \(\displaystyle DK={18}{\small . }\)
Ответ: \(\displaystyle 18{\small .}\)
Второй способ решения
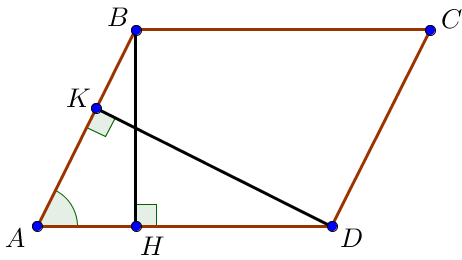
Угол \(\displaystyle A\) – общий для прямоугольных треугольников \(\displaystyle ABH\) и \(\displaystyle ADK \small.\) Также нам известен \(\displaystyle \sin\angle A \small.\)
Поэтому, зная \(\displaystyle \sin \angle A \small,\)
- из треугольника \(\displaystyle ABH\) найдем высоту \(\displaystyle BH \small;\)
- из треугольника \(\displaystyle ADK\) найдем высоту \(\displaystyle DK \small.\)
Сравнивая высоты \(\displaystyle BH\) и \(\displaystyle DK\small,\) получим искомый ответ.
Найдем высоту \(\displaystyle BH\) из прямоугольного треугольника \(\displaystyle ABH{\small.}\)
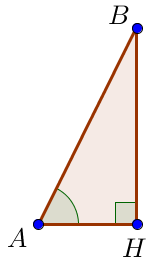
Так как \(\displaystyle \sin \angle A = \frac{BH}{AB}\small,\) то
\(\displaystyle BH=AB\cdot \sin \angle A = 3\cdot \frac{6}{7}=\frac{18}{7} \small.\)
Найдем высоту \(\displaystyle DK\) из прямоугольного треугольника \(\displaystyle ADK{\small.}\)
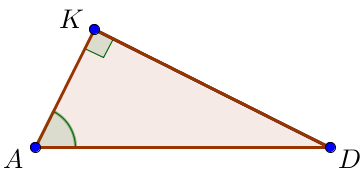
Так как \(\displaystyle \sin \angle A = \frac{DK}{AD} \small,\) то
\(\displaystyle DK=AD\cdot \sin \angle A = 21\cdot \frac{6}{7}=3\cdot 6 = 18 \small.\)
Тогда большая высота равна \(\displaystyle DK={18}{\small . }\)
Ответ: \(\displaystyle 18{\small .}\)