Диагональ параллелограмма образует с двумя его сторонами углы \(\displaystyle 26^\circ\) и \(\displaystyle 34^\circ \small.\) Найдите больший угол параллелограмма. Ответ дайте в градусах.
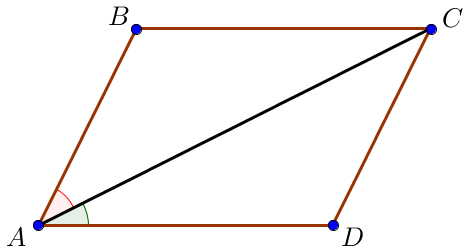
Пусть диагональ \(\displaystyle AC\) образует со стороной \(\displaystyle AD\) угол \(\displaystyle \color{green}{26^\circ } \small,\) а со стороной \(\displaystyle AB\) – угол \(\displaystyle \color{red}{34^\circ} \small.\)
Тогда
\(\displaystyle \color{green}{\angle CAD} = \color{green}{26^\circ } \small,\) \(\displaystyle \color{red}{\angle BAC} = \color{red}{34^\circ }\small.\)
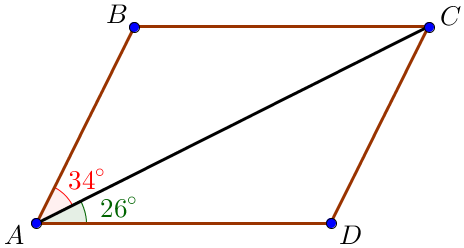
Найдем углы параллелограмма.
\(\displaystyle \color{blue}{\angle BAD} = \color{red}{\angle BAC }+ \color{green}{\angle CAD} = \color{red}{34^\circ }+ \color{green}{26^\circ} = \color{blue}{60^\circ } \small.\)
По свойству параллелограмма сумма углов, прилежащих к одной стороне, равна \(\displaystyle 180^\circ \small.\) Значит,
\(\displaystyle \angle ADC + \color{blue}{\angle BAD }= 180^\circ \small.\)
Тогда
\(\displaystyle \angle ADC = 180^{\circ} - \color{blue}{\angle BAD }= 180^\circ - \color{blue}{60^\circ} = 120^\circ \small.\)
Так как \(\displaystyle 120>60\) , то наибольший угол параллелограмма составляет \(\displaystyle 120^\circ \small.\)
Ответ: \(\displaystyle 120^\circ \small.\)