Найдите \(\displaystyle \sin\, 2\alpha,\) если \(\displaystyle \cos \alpha = \frac{3}{5} \) и \(\displaystyle \alpha \in \left( \frac{3\pi}{2};\ 2\pi \right).\)
Применим формулу синуса двойного угла
\(\displaystyle \sin\, 2\alpha=2\sin\alpha \, \cos \alpha\)
По условию \(\displaystyle \cos \alpha = \frac{3}{5} \). Значит, нужно найти \(\displaystyle \sin \alpha{\small.} \)
Используем основное тригонометрическое тождество.
Для любого \(\displaystyle \alpha\) верно:
\(\displaystyle \cos^2\alpha+\sin^2\alpha=1\)
Отсюда:
\(\displaystyle \sin^2\alpha=1-\cos^2\alpha{\small.}\)
Подставим заданное по условию значение \(\displaystyle \cos \alpha = \frac{3}{5} {:}\)
\(\displaystyle \sin^2\alpha=1-\bigg(\frac{3}{5} \bigg)^2=1-\frac{9}{25}=\frac{16}{25}{\small.}\)
Если \(\displaystyle \sin^2\alpha=\frac{16}{25},\) то
\(\displaystyle \sin\alpha=\pm \sqrt{ \frac{16}{25}}{\small,}\)
\(\displaystyle \sin\alpha=\pm \frac{4}{5}{\small.}\)
Определим, какой именно знак имеет \(\displaystyle \sin\alpha{\small.}\)
По условию \(\displaystyle \alpha \in \left( \frac{3\pi}{2};\ 2\pi \right){\small.}\)
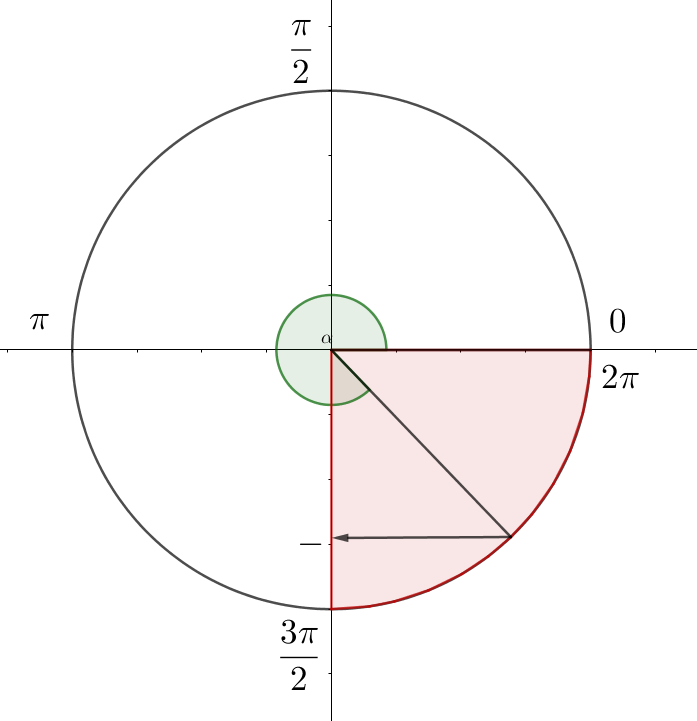
В четвертой четверти значение синуса отрицательно. Следовательно,
\(\displaystyle \sin\alpha=-\frac{4}{5}{\small.}\)
Тогда:
\(\displaystyle \sin\, 2\alpha=2\sin\alpha \, \cos \alpha=2 \cdot \bigg( -\frac{4}{5} \bigg ) \cdot \frac{3}{5}=-\frac{24}{25}=-0{,}96{\small.}\)
Ответ:\(\displaystyle -0{,}96{\small.}\)