Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры от времени работы:\(\displaystyle T(t)=T_0+bt+at^2 , \) где \(\displaystyle t\) – время в минутах, \(\displaystyle T_0=1400 К, a=−10 \) К/мин2, \(\displaystyle b=200 \) К/мин. Известно, что при температуре нагревательного элемента свыше \(\displaystyle 1760 \) К прибор может испортиться, поэтому его нужно отключить. Найдите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ выразите в минутах.
По условию задачи, зависимость температуры от времени работы описывается формулой
\(\displaystyle T(t)=\color{blue}{T_0}+\color{magenta}{b}t+\color{green}{a}t^2{ \small .} \)
Подставим данные значения параметров \(\displaystyle \color{blue}{T_0} = \color{blue}{1400},\) \(\displaystyle \color{green}{a} = \color{green}{- 10}\) и \(\displaystyle \color{magenta}{b}=\color{magenta}{200}{{ \small :}}\)
\(\displaystyle T(t)=\color{blue}{1400}+\color{magenta}{200}\cdot t+\color{green}{(-10)}\cdot t^2{ \small ,} \)
\(\displaystyle T(t)={1400}+200 t-10 t^2{ \small .} \)
По условию должно выполняться ограничение \(\displaystyle T \leq 1760 { \small .}\)
Значит, выполняется неравенство
\(\displaystyle {1400}+200 t-10 t^2\leq 1760{ \small .} \)
Решим это неравенство методом интервалов.
Преобразуем неравенство так, чтобы с одной стороны был ноль:
\(\displaystyle {1400}+200 t-10 t^2\leq 1760 { \small ,} \)
\(\displaystyle {1400}+200 t-10 t^2-1760 \leq 0{ \small ,} \)
\(\displaystyle -10 t^2+200 t-360 \leq 0{ \small .}\)
Разделим обе части неравенства на \(\displaystyle - 10.\) Поскольку \(\displaystyle -10<0,\) то знак неравенства меняется на противоположный:
\(\displaystyle -10 t^2+200 t-360 \leq 0 \,| :(\color{red}{ -10}){ \small .}\)
\(\displaystyle t^2-20 t+36 \geq 0{ \small .}\)
Найдем корни уравнения \(\displaystyle t^2-20 t+36 = 0{ \small .}\)
Отметим найденные корни на числовой прямой, закрашивая их (так как знак неравенства нестрогий):

Получаем три интервала:
\(\displaystyle (-\infty;2){ \small ,} \, (2;18)\) и \(\displaystyle (18;+\infty){\small .}\)
Определим знак функции \(\displaystyle f(t)= t^2-20 t+36\) на каждом из данных интервалов.
Расставим знаки на интервалах:
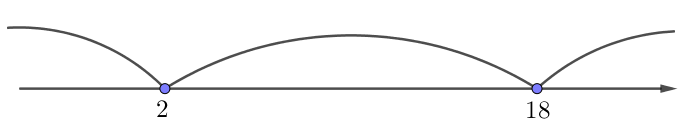
Тогда неравенство \(\displaystyle t^2-20 t+36 \geq 0\) имеет решение
\(\displaystyle t\in (-\infty ;2]\cup [18;+\infty ){\small .}\)
При полученных значениях \(\displaystyle t\)температура нагревательного элемента не будет превосходить \(\displaystyle 1760\) К.
Через \(\displaystyle 2\)минуты после начала работы прибора температура нагревательного элемента станет равной \(\displaystyle 1760\)К и при дальнейшей эксплуатации превзойдет значение в \(\displaystyle 1760\)К. Тогда наибольшее допустимое значение \(\displaystyle t\)составляет \(\displaystyle 2\)мин.
Ответ: \(\displaystyle 2\)мин.