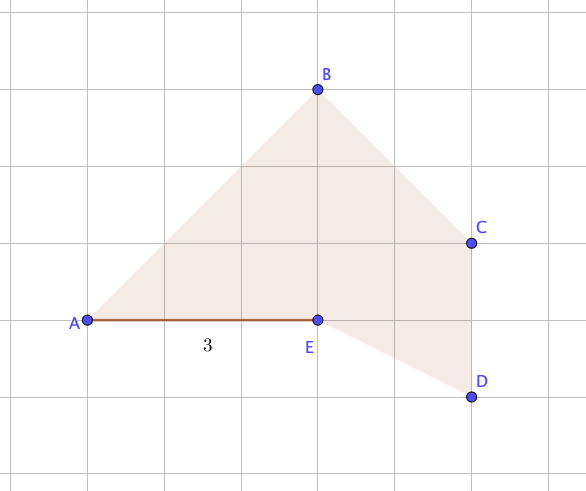
Найдите периметр фигуры, если нанесена сетка из единичных квадратов:
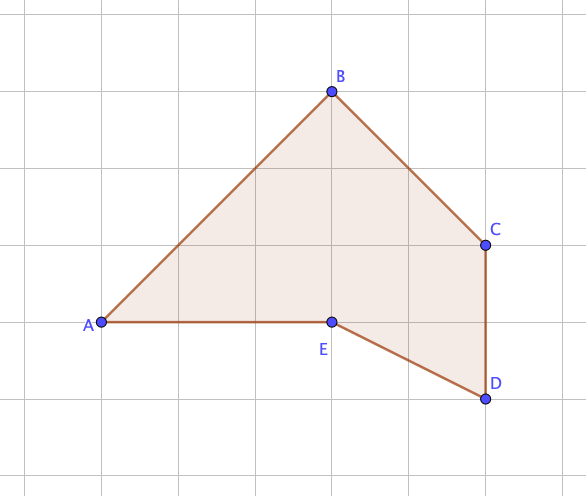
Найдем длину каждой стороны.

\(\displaystyle AB\) – гипотенуза в прямоугольном треугольнике, с катетами, равными \(\displaystyle 3{\small .}\)
Тогда по теореме Пифагора
\(\displaystyle AB=\sqrt{3^2+3^2}=\sqrt{2\cdot 3^2}=3\sqrt{2}{\small .}\)
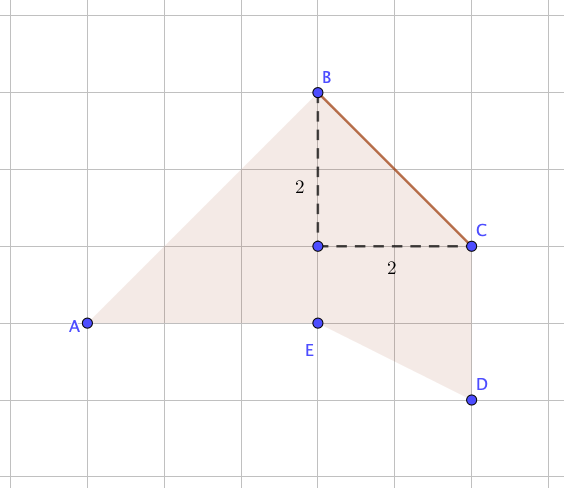
\(\displaystyle BC\) – гипотенуза в прямоугольном треугольнике, с катетами, равными \(\displaystyle 2{\small .}\)
Тогда по теореме Пифагора
\(\displaystyle BC=\sqrt{2^2+2^2}=\sqrt{2\cdot 2^2}=2\sqrt{2}{\small .}\)
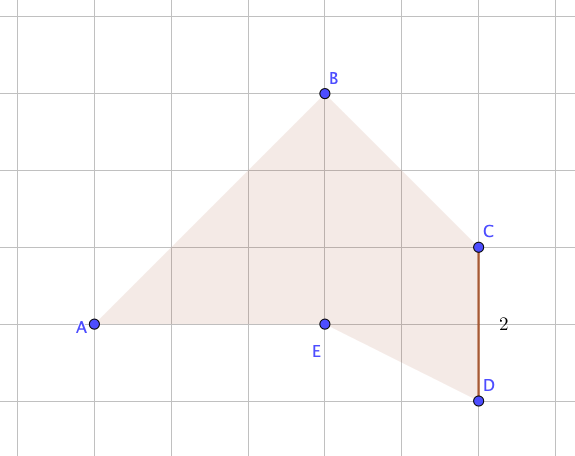
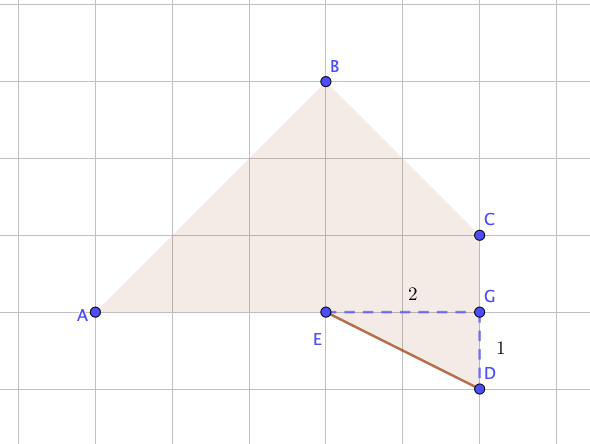
\(\displaystyle DE\) – гипотенуза в прямоугольном треугольнике, с катетами, равными \(\displaystyle 1\) и \(\displaystyle 2{\small .}\)
Тогда по теореме Пифагора
\(\displaystyle DE=\sqrt{1^2+2^2}=\sqrt{5}{\small .}\)
Таким образом, имеем:
Следовательно, периметр многоугольника равен
\(\displaystyle \begin{aligned} AB+BC+CD+DE+EA&=3\sqrt{2}+2\sqrt{2}+2+\sqrt{5}+3=\\&=5+5\sqrt{2}+\sqrt{5}{\small .}\end{aligned}\)
Ответ: \(\displaystyle 5+5\sqrt{2}+\sqrt{5}{\small .}\)