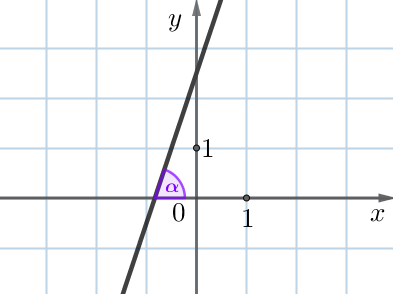
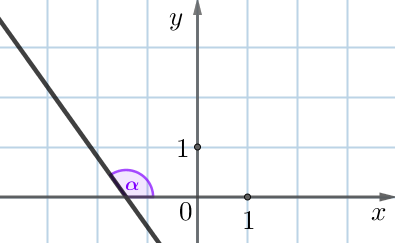
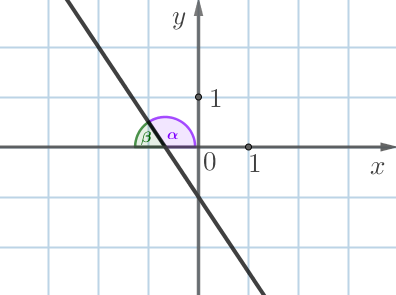
На рисунке изображена прямая – график линейной функции \(\displaystyle y=kx+b {\small .}\) Найдите \(\displaystyle k {\small .}\)
Чтобы найти \(\displaystyle \tg \color{green}{\beta}{ \small ,}\) постройте прямоугольный треугольник с целочисленными катетами и углом, равным \(\displaystyle \color{green}{\beta}{\small .}\) Для этого перетащите мышкой оранжевые точки в узлы сетки.
| \(\displaystyle k=\tg \color{#6600CC}{\alpha}\,= -\tg \color{#006400}{ \beta }= - \) | \(\displaystyle =\) |
Угловой коэффициент \(\displaystyle k\) прямой \(\displaystyle y=kx+b \) найдём по формуле:
\(\displaystyle k=\tg \, \color{#6600CC}{\alpha}\,= -\tg \, \color{green}{\beta}{\small .}\)
1. Построим прямоугольный треугольник с целочисленными катетами и углом, равным \(\displaystyle \color{green}{\beta} {\small .}\)
Передвинем оранжевые точки так, чтобы у них оказались целочисленные координаты.
Получили (один из возможных) прямоугольных треугольников \(\displaystyle ABC {\small :}\)
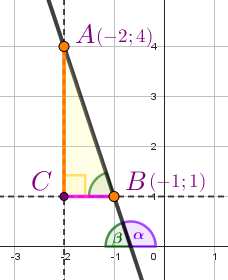
Заметим, что углы \(\displaystyle ABC\) и \(\displaystyle \color{green}{\beta} {\small}\) равны как соответственные углы при пересечении параллельных прямых секущей. Поэтому
\(\displaystyle \tg \color{green}{\beta} = \tg \angle ABC {\small .}\)
2. Вычислим тангенс угла \(\displaystyle ABC\) в полученном треугольнике.
Он равен отношению противолежащего катета \(\displaystyle \color{DarkOrange}{AC}\) к прилежащему \(\displaystyle \color{magenta}{OC} {\small .}\)
Определим по рисунку длины катетов.
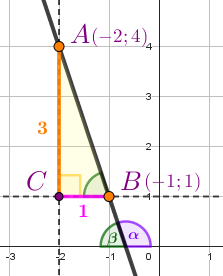
\(\displaystyle \color{DarkOrange} {AC}=\color{DarkOrange}{3}\) и \(\displaystyle \color{magenta} {BC}=\color{magenta}{1} {\small .} \)
Тогда:
\(\displaystyle \tg \angle ABC\,=\frac{\color{DarkOrange} {AC}}{\color{magenta} {BC}} = \frac{\color{DarkOrange} 3}{\color{magenta} 1}=3{\small .}\)
3. Теперь можем найти угловой коэффициент прямой:
\(\displaystyle k=\tg \color{#6600CC}{\alpha}=-\tg \color{green}{\beta}=-\tg \angle ABC=-3{\small .}\)
Ответ: \(\displaystyle k=\tg \color{#6600CC}{\alpha}=-\tg \color{green}{\beta}=- \frac{3}{1}=-3{\small .}\)