При подозрении на наличие некоторого заболевания пациента отправляют на ПЦР-тест. Если заболевание действительно есть, то тест подтверждает его в \(\displaystyle 72\%\) случаев. Если заболевания нет, то тест выявляет отсутствие заболевания в среднем в \(\displaystyle 95\%\) случаев. Известно, что в среднем тест оказывается положительным у \(\displaystyle 15\%\) пациентов, направленных на тестирование. При обследовании некоторого пациента врач направил его на ПЦР-тест, который оказался положительным. Какова вероятность того, что пациент действительно имеет это заболевание?
Найдите вероятность события "пациент болен, если результат теста оказался положительным":
результат округлите до сотых
Обозначим события:
- \(\displaystyle A_1\) – пациент болен,
- \(\displaystyle A_2\) – пациент здоров,
- \(\displaystyle B_1\) – результат теста положителен,
- \(\displaystyle B_2\) – результат теста отрицателен.
Посчитаем вероятности \(\displaystyle P(B_1)\) и \(\displaystyle P(B_2){\small :}\)
- по условию \(\displaystyle P(B_1)=0{,}15\) (вероятность того, что результат теста положителен);
- тогда \(\displaystyle P(B_2)=1-0{,}15=0{,}85\) (вероятность того, что результат теста отрицателен).
По условию задачи известно:
- Если пациент болен, то вероятность положительного теста равна \(\displaystyle 0{,}72\small.\) Значит, вероятность отрицательного теста у больного человека равна \(\displaystyle 1-0{,}72=0{,}28\small.\)
То есть
\(\displaystyle P_{A_1}(B_1)=0{,}72\) (условная вероятность "результат теста положителен, если пациент болен");
\(\displaystyle P_{A_1}(B_2)=0{,}28 \) (условная вероятность "результат теста отрицателен, если пациент болен").
- Если пациент здоров, то результат теста будет отрицательным с вероятностью \(\displaystyle 0{,}95\small.\) Значит, вероятность положительного теста у здорового человека равна \(\displaystyle 1-0{,}95=0{,}05\small.\)
То есть
\(\displaystyle P_{A_2}(B_2)=0{,}95\) (условная вероятность "результат теста отрицателен, если пациент здоров");
\(\displaystyle P_{A_2}(B_1)=0{,}05\) (условная вероятность "результат теста положителен, если пациент здоров").
Найдем значение \(\displaystyle P(A_1)\).
Используем для нахождения известное значение \(\displaystyle P(B_1){ \small ,}\) расписав его по формуле полной вероятности.
Введем обозначения:
- пусть\(\displaystyle P(A_1)=x\) (вероятность того, что пациент болен);
- тогда \(\displaystyle P(A_2)=1-x\) (вероятность того, что пациент здоров).
Построим для события \(\displaystyle B_1 \) для наглядности граф возможных исходов, на котором обозначим все вероятности:
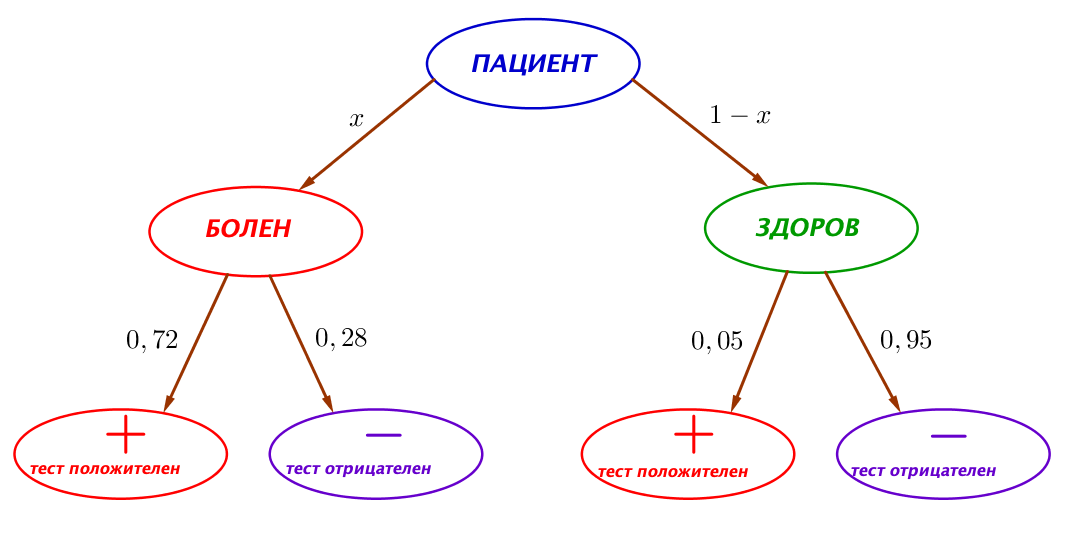
По графу видим, что для положительного теста благоприятны два пути:
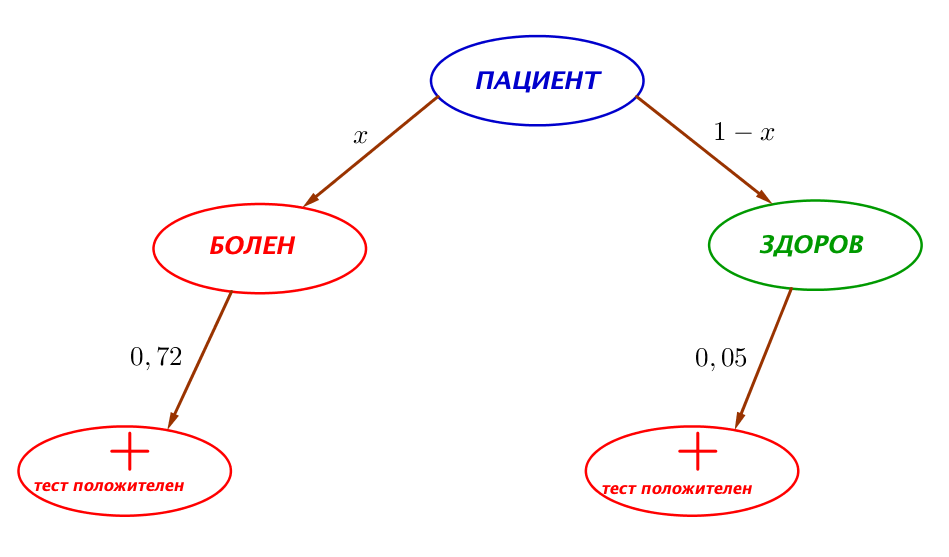
- Первый путь (левая ветка графа) соответствует событию "пациент болен и тест положителен". Запишем вероятность этого события:
\(\displaystyle \\ \)\(\displaystyle P(\text{\scriptsize пациент болен и результат теста положительный})=\color{red}{P(A_1) \cdot P_{A_1}(B_1)} {\small.}\) \(\displaystyle \\ \)
- Второй путь (правая ветка графа) соответствует событию "пациент здоров и тест положителен". Запишем вероятность этого события:
\(\displaystyle \\ \) \(\displaystyle P(\text{\scriptsize пациент здоров и результат теста положительный})=\color{green}{P(A_2) \cdot P_{A_2}(B_1)} {\small.}\)
Полная вероятность события \(\displaystyle B_1\)(результат теста положителен) равна сумме вероятностей:
\(\displaystyle P(B_1)=\color{red}{P(A_1) \cdot P_{A_1}(B_1)}+\color{green}{P(A_2) \cdot P_{A_2}(B_1)} \small.\) \(\displaystyle \\ \)
Подставим числовые значения в полученную формулу:
\(\displaystyle 0{,}15= x \cdot 0{,}72+(1-x) \cdot 0{,}05\small.\)
Решая это уравнение, найдем \(\displaystyle x\small:\)
\(\displaystyle 0{,}15=0{,}72\cdot x+0{,}05-0{,}05\cdot x\small,\)
\(\displaystyle 0{,}67 \cdot x=0{,}1\small,\)
\(\displaystyle x=\frac{0{,}1}{0{,}67}=\frac{10}{67}\small.\)
Значит,
\(\displaystyle P(A_1)=\frac{10}{67}\small.\)
Вычислим искомую вероятность события "пациент болен, если результат теста оказался положительным".
Для этого рассмотрим событие "пациент болен и тест положителен"="тест положителен и пациент болен" двумя способами:
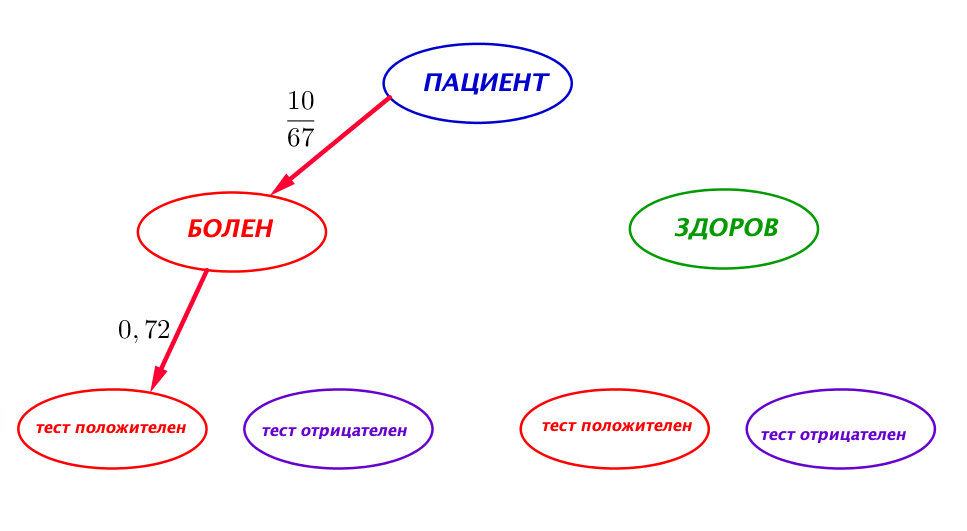 | 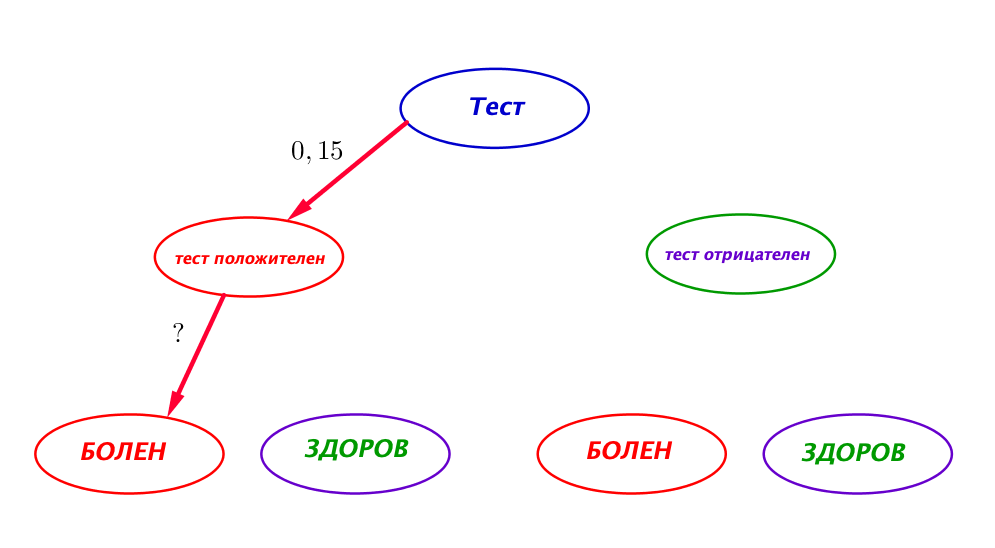 |
| \(\displaystyle \frac{10}{67} \cdot 0,72\) | \(\displaystyle 0,15 \cdot \Large{?} \) |
Получаем:
\(\displaystyle \frac{10}{67} \cdot 0,72= 0,15 \cdot \Large{?}, \)
то есть
\(\displaystyle \frac{10}{67} \cdot 0,72= 0,15 \cdot P_{B_1}(A_1){\small,}\)
\(\displaystyle P_{B_1}(A_1)=\frac{10}{67} \cdot \frac{72}{100}:\frac{15}{100}\approx 0{,}72 {\small.}\)
Ответ: \(\displaystyle 0{,}72 \small.\)