На координатной прямой отмечены числа \(\displaystyle m\) и \(\displaystyle n\) и точки \(\displaystyle A\) и \(\displaystyle B{\small .}\)
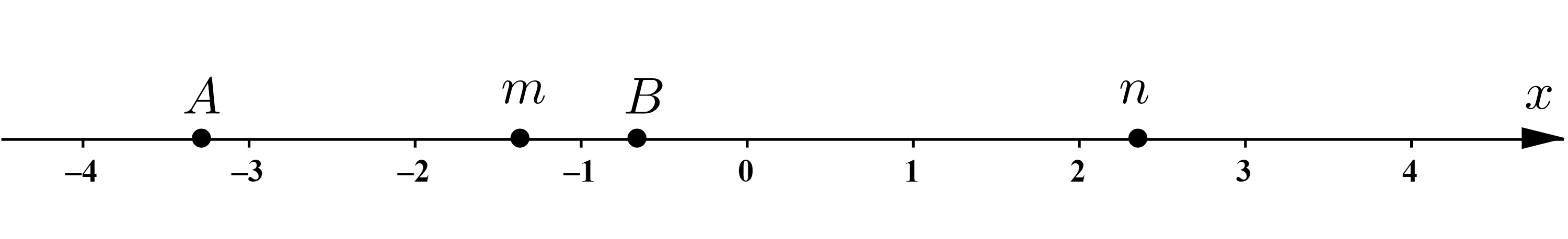
Каждой точке соответствует одно из чисел в правом столбце.
Установите соответствие между указанными точками и числами:
Число \(\displaystyle mn\) соответствует точке
Число \(\displaystyle \frac{1}{n}+m\) соответствует точке
Оценим по рисунку числа \(\displaystyle m\) и \(\displaystyle n{\small :}\)
\(\displaystyle \color{blue}{-2}<\color{blue}{m}<\color{blue}{-1}{\small ,}\)
\(\displaystyle \color{green}{2}<\color{green}{n}<\color{green}{3}{\small .}\)
Определим, какой точке соответствует число \(\displaystyle \frac{1}{n}+m{\small .}\)
Сначала оценим \(\displaystyle \frac{1}{n}{\small .}\)
Так как \(\displaystyle 2<n<3{\small ,}\) то для обратных чисел верно неравенство с противоположными знаками:
\(\displaystyle \frac{1}{2}>\frac{1}{n}>\frac{1}{3}{\small .}\)
Для удобства вычислений будем пользоваться менее точной оценкой:
\(\displaystyle 0<\frac{1}{n}<1{\small .}\)
Теперь оценим число \(\displaystyle m+\frac{1}{n}{\small .}\)
Для этого почленно сложим неравенства \(\displaystyle \color{blue}{-2}<\color{blue}{m}<\color{blue}{-1}\) и \(\displaystyle \color{red}{0}<\color{red}{\frac{1}{n}}<\color{red}{1}{\small :}\)
\(\displaystyle \color{blue}{-2}+\color{red}{0}<\color{blue}{m}+\color{red}{\frac{1}{n}}<\color{blue}{-1}+\color{red}{1}{\small,}\)
\(\displaystyle -2<m+\frac{1}{n}<0{\small .}\)
Среди точек \(\displaystyle A{\small ,}\)\(\displaystyle B\) только точка \(\displaystyle B\) расположена в промежутке от \(\displaystyle -2\) до \(\displaystyle 0{\small .}\)
Следовательно, точка \(\displaystyle B\) соответствует числу \(\displaystyle m+\frac{1}{n}{\small .}\)
Значит, оставшаяся точка \(\displaystyle A\) соответствует оставшемуся числу \(\displaystyle mn{\small .}\)
| число \(\displaystyle mn\) соответствует точке \(\displaystyle A{\small ,}\) |
| число \(\displaystyle \frac{1}{n}+m\) соответствует точке \(\displaystyle B{\small .}\) |