В выпуклом четырёхугольнике \(\displaystyle ABCD\) углы \(\displaystyle CDB\) и \(\displaystyle CAB\) равны.
\(\displaystyle a) \) Докажите, что углы \(\displaystyle DAC\) и \(\displaystyle DBC\) также равны.
\(\displaystyle б)\) Найдите величину угла \(\displaystyle CAD {\small,}\) если \(\displaystyle \angle BDC=60^{\circ}{\small,}\) \(\displaystyle \angle BCD=98^{\circ}{\small.}\) Ответ дайте в градусах.
Ознакомьтесь с решением аналогичной задачи:
В выпуклом четырёхугольнике \(\displaystyle ABCD\) углы \(\displaystyle DAC\) и \(\displaystyle DBC\) равны.
\(\displaystyle a) \) Докажите, что углы \(\displaystyle CDB\) и \(\displaystyle CAB\) также равны.
\(\displaystyle б)\) Найдите величину угла \(\displaystyle BAC {\small,}\) если \(\displaystyle \angle CBD=67^{\circ}{\small,}\) \(\displaystyle \angle BCD=94^{\circ}{\small.}\) Ответ дайте в градусах.
Решение.
\(\displaystyle a) \) По условию задачи выполним чертёж.
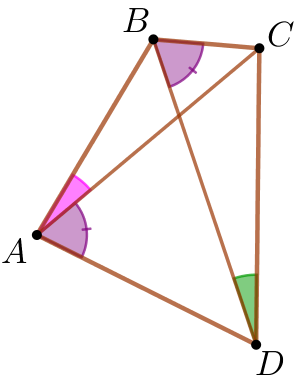 | \(\displaystyle ABCD\)– выпуклый четырёхугольник. \(\displaystyle \angle DAC=\angle DBC{\small.}\)
Требуется доказать, что углы \(\displaystyle CDB\) и \(\displaystyle CAB\) равны. |
Вокруг любого треугольника можно описать окружность и притом только одну.
Радиус описанной окружности можно найти по теореме синусов.
Теорема синусов
\(\displaystyle \frac{\color{Purple}{a}}{\sin(\angle A)}=\frac{\color{green}{b}}{\sin(\angle B)}=\frac{\color{blue}{c}}{\cos(\angle C)}=2\color{red}{R}{\small,}\) где \(\displaystyle \color{red}{R}\) – радиус описанной окружности. |
Рассмотрим треугольники \(\displaystyle ACD\) и \(\displaystyle BCD{\small.}\)
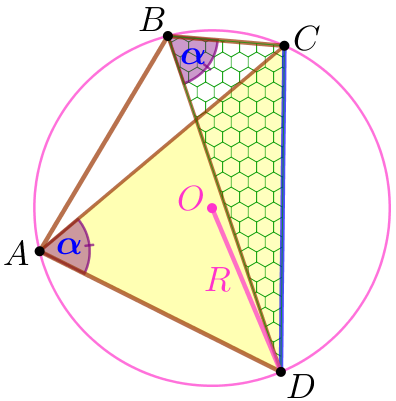 |
По теореме синусов радиус окружности, описанной вокруг треугольника \(\displaystyle ACD{\small,}\) равен радиусу окружности, описанной вокруг треугольника \(\displaystyle BCD\) и равен \(\displaystyle R=\frac{CD}{2 \cdot \sin\alpha} {\small.}\) |
Значит, точки \(\displaystyle A{\small,}\,B{\small,}\,C{\small,}\,D\) лежат на одной окружности.
Получили, что четырёхугольник \(\displaystyle ABCD\) вписан в окружность.
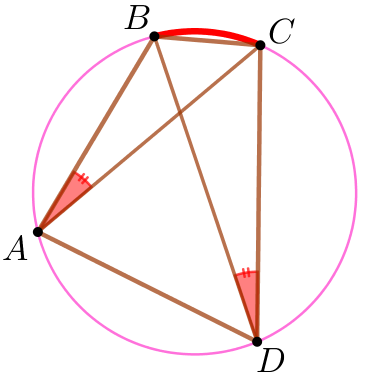 | В окружности вписанные углы, опирающиеся на одну дугу, равны. Вписанные углы \(\displaystyle CDB\) и \(\displaystyle CAB\) опираются на одну дугу \(\displaystyle \overset{\smile}{BC} {\small.}\) Значит, \(\displaystyle \angle CDB=\angle CAB{\small.}\) |
Утверждение доказано.
\(\displaystyle б)\) По условию задачи \(\displaystyle \angle CBD=67^{\circ}{\small,}\) \(\displaystyle \angle BCD=94^{\circ}{\small.}\)
Требуется найти величину угла \(\displaystyle BAC {\small.}\)
По доказанному в пункте \(\displaystyle a)\) \(\displaystyle \angle BAC=\angle CDB{\small.}\)
Рассмотрим треугольник \(\displaystyle BCD{\small.}\)
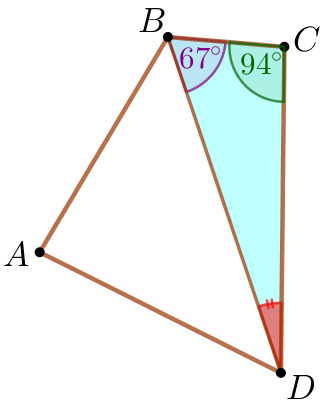 | Сумма внутренних углов треугольника равна \(\displaystyle 180^{\circ} {\small.}\) \(\displaystyle \angle CDB+\angle BCD+\angle CBD=180^{\circ} {\small;}\) \(\displaystyle \angle CDB=180^{\circ}-(\angle BCD+\angle CBD) {\small;}\) \(\displaystyle \angle CDB=180^{\circ}-(94^{\circ}+67^{\circ})= 19^{\circ}{\small.}\) |
Получаем
\(\displaystyle \angle BAC=\angle CDB=19^{\circ}{\small.}\)
Ответ: \(\displaystyle б)\ 19^{\circ} {\small.}\)