Точка \(\displaystyle K\) – середина боковой стороны \(\displaystyle CD\) трапеции \(\displaystyle ABCD {\small.}\)
\(\displaystyle a) \) Докажите, что площадь треугольника \(\displaystyle KAB\) равна половине площади трапеции.
\(\displaystyle б)\) Найдите сумму площадей треугольников \(\displaystyle BKC\) и \(\displaystyle AKD {\small,}\) если площадь трапеции равна \(\displaystyle 46 {\small.}\)
Ознакомьтесь с решением аналогичной задачи:
Точка \(\displaystyle E\) – середина боковой стороны \(\displaystyle AB\) трапеции \(\displaystyle ABCD {\small.}\)
\(\displaystyle a) \) Докажите, что площадь треугольника \(\displaystyle ECD\) равна половине площади трапеции.
\(\displaystyle б)\) Найдите сумму площадей треугольников \(\displaystyle BEC\) и \(\displaystyle AED {\small,}\) если площадь трапеции равна \(\displaystyle 54 {\small.}\)
Решение.
\(\displaystyle a)\) По условию задачи выполним чертёж.
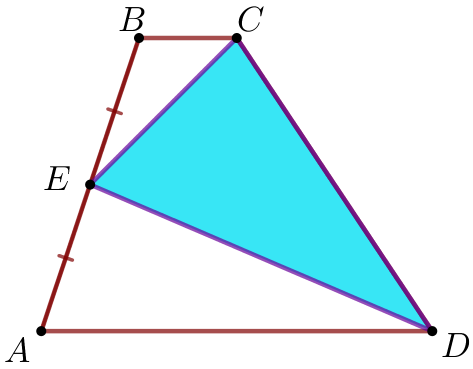 | \(\displaystyle ABCD\) – трапеция; точка \(\displaystyle E\) – середина стороны \(\displaystyle AB{\small,}\) то есть \(\displaystyle AE=BE{\small.}\)
Требуется доказать, что площадь треугольника \(\displaystyle ECD\) равна половине площади трапеции. |
получаем
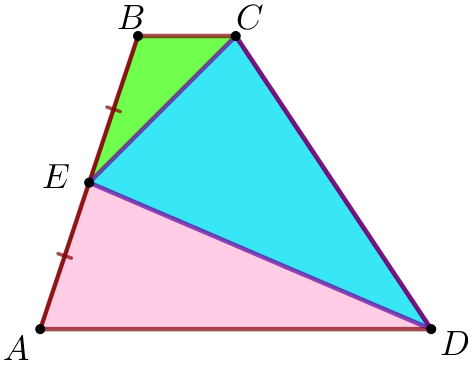 | Так как трапеция состоит из трёх треугольников, то площадь трапеции равна сумме площадей этих треугольников: \(\displaystyle S_{ABCD}=S_{\triangle ECD}+S_{\triangle BEC}+S_{\triangle AED}{\small.}\) Тогда \(\displaystyle S_{\triangle ECD}=S_{ABCD}-(S_{\triangle BEC}+S_{\triangle AED}){\small.}\) |
Выразим сумму площадей треугольников \(\displaystyle BEC\) и \(\displaystyle AED\) через площадь трапеции \(\displaystyle ABCD {\small.}\)
Выполним дополнительное построение.
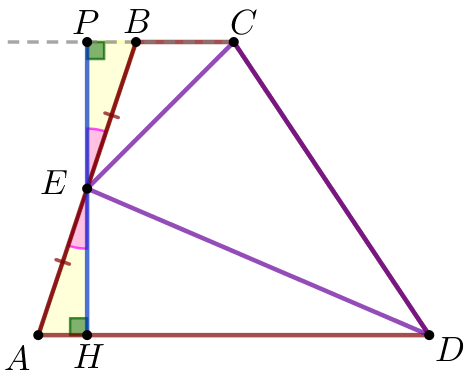 | Через точку \(\displaystyle E\) построим перпендикуляр к основаниям трапеции. Обозначим буквами \(\displaystyle P\) и \(\displaystyle H\) точки пересечения перпендикуляра с прямыми \(\displaystyle BC\) и \(\displaystyle AD\) соответственно. Рассмотрим прямоугольные треугольники \(\displaystyle BEP\) и \(\displaystyle AEH{\small:}\)
Следовательно, \(\displaystyle \triangle BEP=\triangle AEH\) по гипотенузе и острому углу. |
В равных треугольниках соответственные стороны равны. Значит,
\(\displaystyle EP=EH=h {\small.}\)
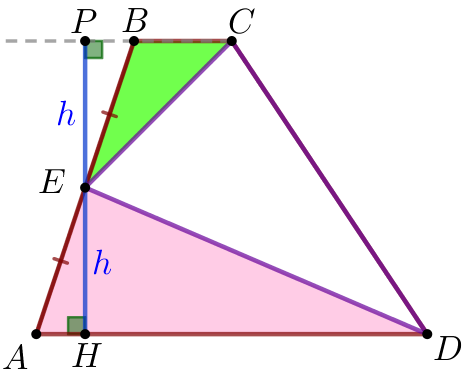 |
|
Тогда
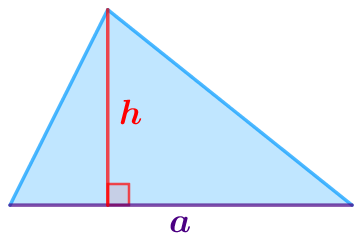
\(\displaystyle S_{\triangle BEC}+S_{\triangle AED}=\frac{1}{2} \cdot BC \cdot h +\frac{1}{2} \cdot AD\cdot h{\small;}\\ \)
\(\displaystyle S_{\triangle BEC}+S_{\triangle AED}=\frac{1}{2} \cdot h \cdot (BC+AD){\small;}\\ \)
\(\displaystyle S_{\triangle BEC}+S_{\triangle AED}=\frac{ (BC+AD)}{2} \cdot h{\small.}\)
\(\displaystyle S_{ABCD}=\frac{BC+AD}{2} \cdot 2 \cdot h {\small.}\)
Значит,
\(\displaystyle S_{\triangle BEC}+S_{\triangle AED}=\frac{1}{2} \cdot S_{ABCD} {\small.}\)
Тогда
\(\displaystyle S_{\triangle ECD}=S_{ABCD}-(S_{\triangle BEC}+S_{\triangle AED}){\small;}\\ \)
\(\displaystyle S_{\triangle ECD}=S_{ABCD}-\frac{1}{2} \cdot S_{ABCD}{\small.}\\ \)
\(\displaystyle S_{\triangle ECD}=\frac{1}{2} \cdot S_{ABCD}{\small.}\\ \)
То есть площадь треугольника \(\displaystyle ECD\) равна половине площади трапеции.
Утверждение доказано.
\(\displaystyle б) \) По условию задачи \(\displaystyle S_{ABCD}=54 {\small.}\)
Требуется найти сумму площадей треугольников \(\displaystyle BEC\) и \(\displaystyle AED {\small.}\)
В пункте \(\displaystyle a)\) получили, что сумма площадей треугольников \(\displaystyle BEC\) и \(\displaystyle AED \) равна половине площади трапеции \(\displaystyle ABCD{\small.}\)
\(\displaystyle S_{\triangle BEC}+S_{\triangle AED}=\frac{1}{2} \cdot S_{ABCD} {\small;}\\ \)
\(\displaystyle S_{\triangle BEC}+S_{\triangle AED}=\frac{1}{2} \cdot 54=27 {\small.}\)
Ответ: \(\displaystyle б) \ 27{\small.} \)