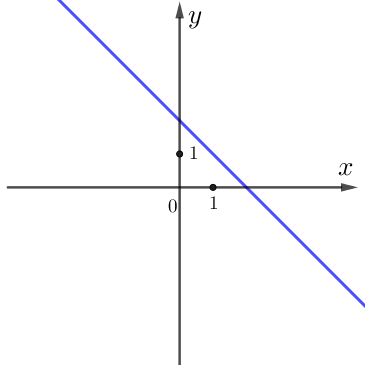
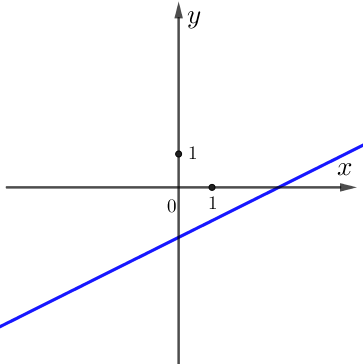
На рисунках изображены графики функций вида \(\displaystyle y=kx+b \small.\)
Установите соответствие между графиками и знаками коэффициентов \(\displaystyle k \small\) и \(\displaystyle b \small.\)
| \(\displaystyle А\) | \(\displaystyle Б\) | \(\displaystyle В\) |
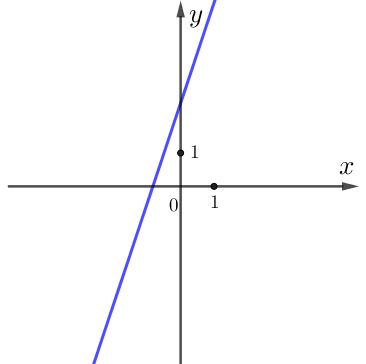 | 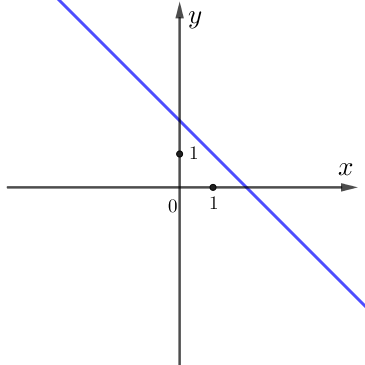 |  |
Даны три прямые, которые являются графиками линейных функций \(\displaystyle y=kx+b \small.\)
Нужно установить соответствие между графиками и знаками коэффициентов \(\displaystyle k \small\) и \(\displaystyle b \small.\)
Каждая пара знаков соответствует одному графику из условия и, каждый график соответствует только одной паре знаков.
Определим знаки коэффициентов \(\displaystyle k\) и \(\displaystyle b\) по графикам \(\displaystyle А\) и \(\displaystyle Б \small.\)
Тогда последняя оставшаяся пара знаков будет соответствовать графику \(\displaystyle В \small.\)
Посмотрим на график функции:
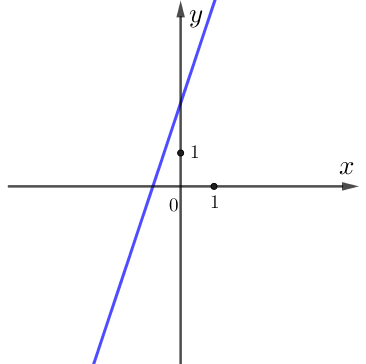
Видим, что:
1. функция возрастает, поэтому \(\displaystyle k>0 {\small ; }\)
2. точка пересечения графика с осью \(\displaystyle Oy{\small }\) лежит выше оси \(\displaystyle Ox{\small ,}\) поэтому её ордината \(\displaystyle b>0 {\small . }\)
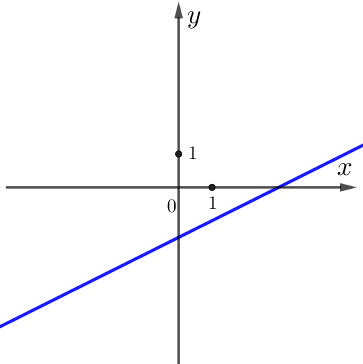
Оставшемуся графику \(\displaystyle В\) соответствует единственная оставшаяся пара знаков \(\displaystyle k>0\) и \(\displaystyle b<0 {\small . }\)
Убедимся в этом.
Занесём полученные результаты в таблицу:
| \(\displaystyle А\) | \(\displaystyle Б\) | \(\displaystyle В\) |
 |  |  |
| \(\displaystyle k>0\) и \(\displaystyle b>0\) | \(\displaystyle k<0\) и \(\displaystyle b>0\) | \(\displaystyle k>0\) и \(\displaystyle b<0\) |