На стороне \(\displaystyle BC\) прямоугольника \(\displaystyle ABCD {\small,}\) у которого \(\displaystyle AB=56\) и \(\displaystyle AD=89 {\small,}\) отмечена точка \(\displaystyle E\) так, что \(\displaystyle \angle EAB=45^{\circ} {\small.}\) Найдите длину отрезка \(\displaystyle ED {\small.}\)
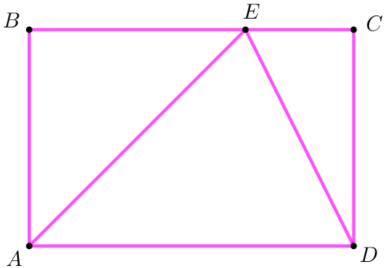
Так как \(\displaystyle ABCD\) – прямоугольник, то \(\displaystyle AB=CD=56 {\small,}\) \(\displaystyle BC=AD=89 {\small.}\)
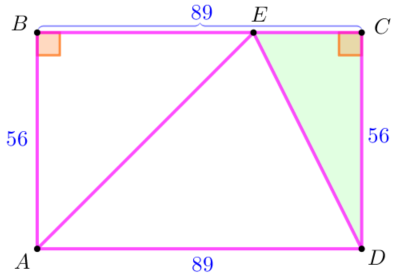 | Требуется найти длину отрезка \(\displaystyle ED {\small.}\) Рассмотрим прямоугольный треугольник \(\displaystyle CDE {\small.}\) По теореме Пифагора \(\displaystyle ED^2=EC^2+CD^2 {\small,}\) \(\displaystyle ED^2=EC^2+56^2 {\small.}\) |
Найдём длину отрезка \(\displaystyle EC {\small.}\)
\(\displaystyle EC=BC-BE=89-BE {\small. }\)
Рассмотрим прямоугольный треугольник \(\displaystyle ABE {\small. }\)
По условию \(\displaystyle \angle EAB =45^{\circ} {\small.}\) Так как сумма острых углов прямоугольного треугольника равна \(\displaystyle 90^{\circ} {\small,}\) то \(\displaystyle \angle BEA=90^{\circ}-\angle EAB =90^{\circ}-45^{\circ}=45^{\circ} {\small.}\) Следовательно, \(\displaystyle \triangle ABE\) – равнобедренный. Тогда \(\displaystyle BE=AB=56 {\small.}\) | 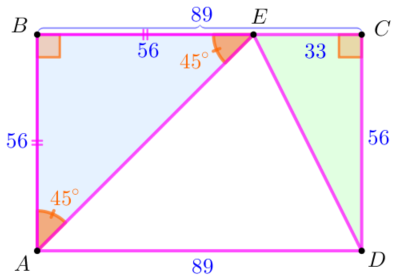 |
Значит,
\(\displaystyle EC=BC-BE=89-56=33 {\small. }\)
Получаем
\(\displaystyle ED^2=EC^2+56^2=33^2+56^2= 1089+3136=4225=65^2{\small.}\)
Так как длина отрезка положительна, то \(\displaystyle ED>0 {\small.}\) Следовательно,
\(\displaystyle ED=65 {\small.}\)
Ответ: \(\displaystyle 65 {\small.}\)