\(\displaystyle ABCDEFGHIJ\) – правильный десятиугольник. Найдите угол \(\displaystyle BCE{\small.}\) Ответ дайте в градусах.
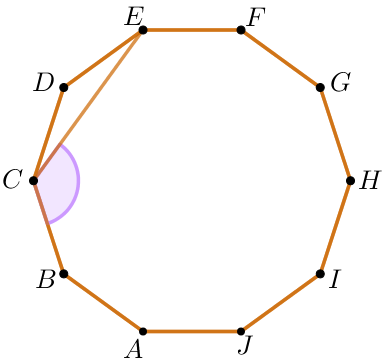
Правильный многоугольник – выпуклый многоугольник, у которого равны все стороны и все углы между смежными сторонами.
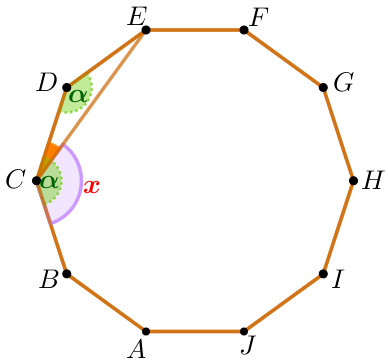 | Пусть угол правильного десятиугольника равен \(\displaystyle \color{darkgreen} \alpha \) и \(\displaystyle \angle BCE = \color{red}x {\small.}\) Тогда \(\displaystyle \color{red}x= \color{darkgreen} \alpha- \angle DCE{\small.}\)
Найдем углы \(\displaystyle \color{darkgreen} \alpha \) и \(\displaystyle \angle DCE{\small.}\) |
Воспользуемся формулой.
Угол при вершине правильного многоугольника равен \(\displaystyle \alpha_{n}=\frac{n-2}{n}\cdot 180^{\circ}{\small ,}\) где
\(\displaystyle n\) – количество сторон правильного многоугольника.
По условию \(\displaystyle n=10 {\small.}\) Получаем \(\displaystyle \color{darkgreen} \alpha=\frac{n-2}{n}\cdot 180^{\circ}{\small ,} \\ \) \(\displaystyle \color{darkgreen} \alpha=\frac{10-2}{10}\cdot 180^{\circ}=\frac{8}{10}\cdot 180^{\circ}=144^{\circ}{\small .}\)
Значит, \(\displaystyle \angle BCD=\angle CDE=\color{darkgreen} \alpha =144^{\circ}{\small.}\) | 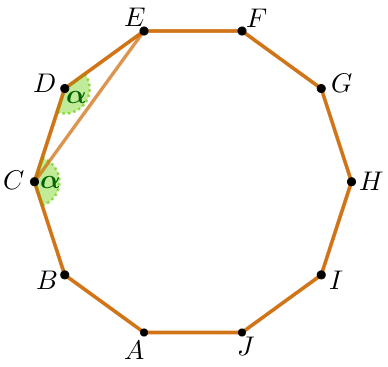 |
Рассмотрим треугольник \(\displaystyle CDE {\small. }\)
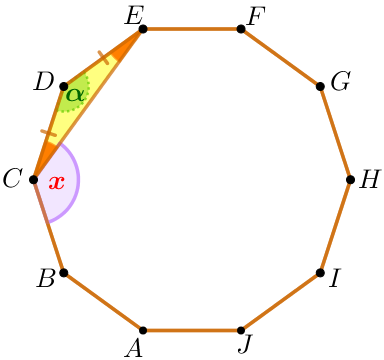 | Так как стороны правильного многоугольника равны, то \(\displaystyle DC=DE {\small.}\) Значит, треугольник \(\displaystyle CDE\) – равнобедренный. В равнобедренном треугольнике углы при основании равны. Сумма внутренних углов треугольника равна \(\displaystyle 180^{\circ}{\small .} \) Тогда \(\displaystyle \angle DCE= \angle DEC=\frac{180^{\circ}-\color{darkgreen} \alpha }{2} {\small ,} \\ \) \(\displaystyle \angle DCE= \frac{180^{\circ}-144^{\circ}}{2}=\frac{36^{\circ}}{2}=18^{\circ} {\small .} \) |
Получаем
\(\displaystyle \color{red}x= \color{darkgreen} \alpha- \angle DCE=144^{\circ}-18^{\circ}=126^{\circ}{\small.}\)
Ответ: \(\displaystyle 126{\small.}\)