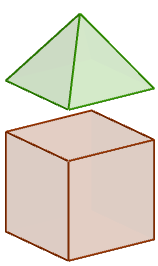
К кубу с ребром \(\displaystyle 1\) приклеили правильную четырёхугольную пирамиду с ребром \(\displaystyle 1\) так, что квадратные грани совпали. Сколько рёбер у получившегося многогранника (невидимые рёбра на рисунке не изображены)?
1 способ
По условию даны:
|
| Куб и пирамиду склеили так, что их основания – квадраты совпали. Таким образом, получили многогранник: |
Количество рёбер полученного многогранника складывается из:
|
Итого:
\(\displaystyle \color{Green}4+\color{red}4+\color{brown}4+\color{blue}4=16 \small. \)
Ответ:\(\displaystyle 16 \small. \)
2 способ
До склеивания общее число рёбер у куба и пирамиды равно:
\(\displaystyle \color{brown}{12}+\color{Green}8=20\small.\)
При склеивании рёбра оснований совместятся, поэтому общее число рёбер уменьшится на \(\displaystyle 4\small.\)
Таким образом, количество рёбер нового многогранника будет равно:
\(\displaystyle \color{brown}{12}+\color{Green}8-4=16\small.\)
Ответ:\(\displaystyle 16 \small. \)