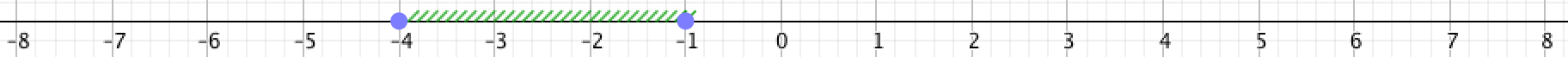Запишите числовой промежуток по изображенному на графике расположению точек:
| \(\displaystyle 1)\) |
|
| \(\displaystyle 2)\) |
|
| \(\displaystyle 3)\) |
|
| \(\displaystyle 4)\) |
|
На рисунке выделены все точки между \(\displaystyle -4\) и \(\displaystyle -1{\small , } \) включая \(\displaystyle -4 \) и включая \(\displaystyle -1{\small : } \)
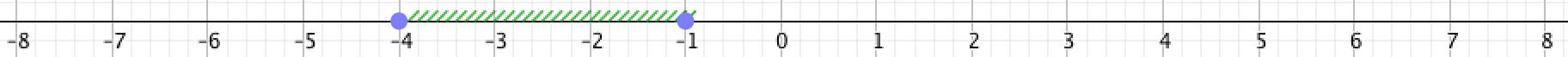
То есть изображены все точки, координаты которых больше либо равны \(\displaystyle -4 \) и меньше либо равны \(\displaystyle -1{\small .}\) Другими словами, это все точки c координатой \(\displaystyle x\) такой, что \(\displaystyle -4\le x \le -1{\small .}\) Такое множество обозначается как \(\displaystyle [-4{\small ; }\,-1]{\small . } \)
Таким образом, искомый числовой промежуток:
\(\displaystyle x \in [-4{\small ; }\,-1]{\small . } \)
Ответ: \(\displaystyle x \in [-4{\small ; }\,-1]{\small . } \)
На рисунке выделены все точки между \(\displaystyle -1\) и \(\displaystyle 2{\small , } \) не включая \(\displaystyle -1 \) и не включая \(\displaystyle 2{\small : } \)

То есть изображены все точки, координаты которых больше \(\displaystyle -1 \) и меньше \(\displaystyle 2{\small .}\)
Другими словами, это все точки c координатой \(\displaystyle x\) такой, что \(\displaystyle -1<x < 2{\small .}\) Такое множество обозначается как \(\displaystyle (-1{\small ; }\,2){\small . } \)
Таким образом, искомый числовой промежуток:
\(\displaystyle x \in (-1{\small ; }\,2){\small . } \)
Ответ: \(\displaystyle x \in (-1{\small ; }\,2){\small . } \)
На рисунке выделены все точки между \(\displaystyle 3\) и \(\displaystyle 4{\small , } \) не включая \(\displaystyle 3 \) и включая \(\displaystyle 4{\small : } \)
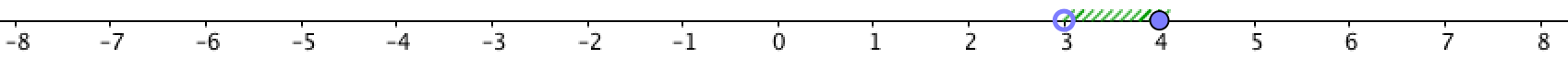
То есть изображены все точки, координаты которых больше \(\displaystyle 3 \) и меньше либо равны \(\displaystyle 4{\small .}\)
Другими словами, это все точки c координатой \(\displaystyle x\) такой, что \(\displaystyle 3<x \le 4{\small .}\) Такое множество обозначается как \(\displaystyle (3{\small ; }\,4]{\small . } \)
Таким образом, искомый числовой промежуток:
\(\displaystyle x \in (3{\small ; }\,4]{\small . } \)
Ответ: \(\displaystyle x \in (3{\small ; }\,4]{\small . } \)
На рисунке выделены все точки между \(\displaystyle -4\) и \(\displaystyle -1{\small , } \) включая \(\displaystyle -4 \) и не включая \(\displaystyle -1{\small : } \)

То есть изображены все точки, координаты которых больше либо равны \(\displaystyle -4 \) и меньше \(\displaystyle -1{\small .}\)
Другими словами, это все точки c координатой \(\displaystyle x\) такой, что \(\displaystyle -4\le x <-1{\small .}\) Такое множество обозначается как \(\displaystyle [-4{\small ; }\,-1){\small . } \)
Таким образом, искомый числовой промежуток:
\(\displaystyle x \in [-4{\small ; }\,-1){\small . } \)
Ответ: \(\displaystyle x \in [-4{\small ; }\,-1){\small . } \)