Катеты прямоугольного треугольника равны \(\displaystyle 6\) и \(\displaystyle 8 \small.\) Найдите радиус вписанной окружности.
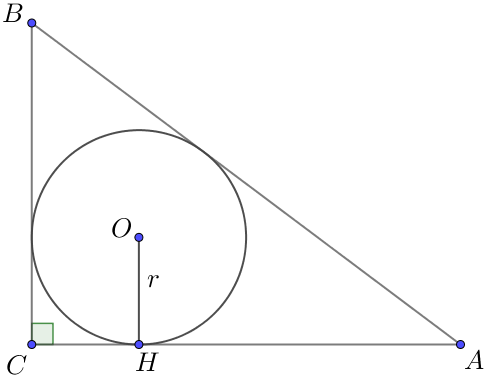
Пусть \(\displaystyle AC=8\) и \(\displaystyle BC=6\) – катеты прямоугольного треугольника \(\displaystyle ABC \small.\)
Из прямоугольного треугольника \(\displaystyle ABC\) по теореме Пифагора
\(\displaystyle AB^2=BC^2+AC^2 \small.\)
Тогда
\(\displaystyle AB^2=6^2+8^2=36+64=100 \small.\)
Поскольку длина отрезка положительна, то \(\displaystyle AB=10 \small.\)
В прямоугольном треугольнике \(\displaystyle ABC\) найдем площадь и полупериметр:
\(\displaystyle S=\frac{1}{2} \cdot AC \cdot BC= \frac{1}{2} \cdot 8 \cdot 6=24 \small, \\ \)
\(\displaystyle p=\frac{AB+BC+AC}{2}=\frac{10+6+8}{2}=12. \small\)
По формуле
Площадь треугольника через радиус вписанной окружности
\(\displaystyle S=pr\)
получаем:
\(\displaystyle 24={12}\cdot r{\small ,} \)
\(\displaystyle r=2{\small .} \)
Ответ: \(\displaystyle 2 {\small .}\)