Задание
Правило
Алгоритм нахождения точек экстремума дифференцируемой функции
- Находим производную функции и приравниваем к нулю.
- Находим точки, в которых производная равна нулю.
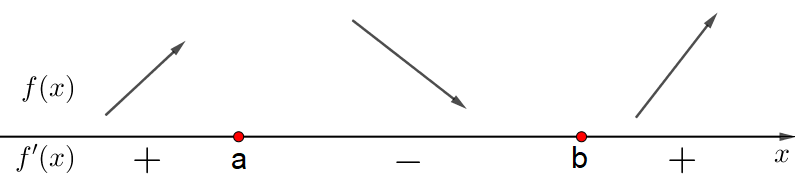
- Отмечаем корни производной на числовой прямой, а также определяем ее знаки на получившихся интервалах.
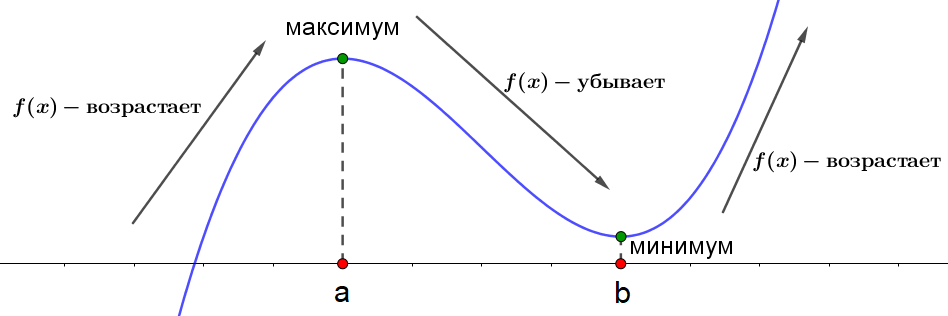
- Если производная меняет в найденной точке знак с \(\displaystyle +\) на \(\displaystyle -{\small ,}\)
то эта точка – точка максимума.
Если производная меняет в найденной точке знак с \(\displaystyle -\) на \(\displaystyle +{\small ,}\)
то эта точка – точка минимума.
Правило
Нахождение наибольшего и наименьшего значения непрерывной функции на отрезке
Непрерывная функция достигает своего наибольшего/наименьшего значения или в точке максимума/минимума на этом отрезке, или на границах отрезка.
Правило
Алгоритм нахождения наибольшего/наименьшего значения дифференцируемой функции на отрезке
- Найти точки максимума/минимума, принадлежащие этому отрезку.
- Вычислить значение функции в точках максимума/минимума.
- Вычислить значение функции на концах отрезка.
- Выбрать наибольшее/наименьшее из полученных чисел.
Решение