В равнобедренной трапеции диагонали перпендикулярны. Средняя линия трапеции равна \(\displaystyle 8{\small .}\) Найдите её высоту.
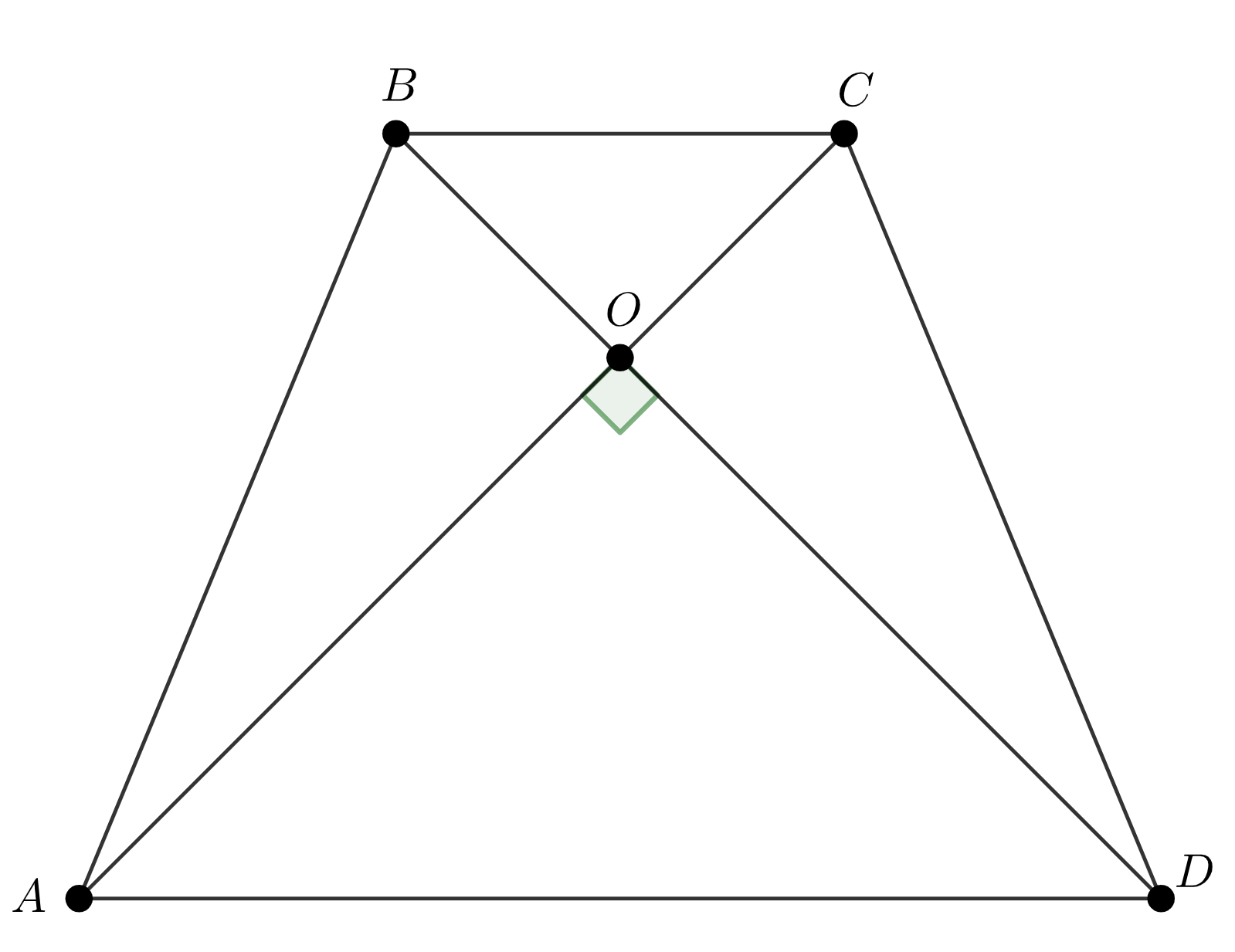
Так как средняя линия трапеции равна полусумме оснований, то сумма оснований равна \(\displaystyle 16{\small .}\)
Первый способ решения
Рассмотрим треугольники \(\displaystyle ABD\) и \(\displaystyle ACD{\small .}\) Они равны по трем сторонам:
Значит, углы \(\displaystyle ADB\) и \(\displaystyle DAC\) равны. Поскольку \(\displaystyle \angle AOD=90^{\circ}{\small ,}\) то из треугольника \(\displaystyle AOD\) получаем: \(\displaystyle \begin{aligned}\angle ADO&=\angle DAO= \frac{1}{2}(180^{\circ} - \angle AOD)=\\&=\frac{1}{2}(180^{\circ} - 90^{\circ})=\frac{1}{2}\cdot 90^{\circ} = 45^{\circ}{\small .}\end{aligned}\) Аналогично, треугольники \(\displaystyle ABC\) и \(\displaystyle BCD\) равны по трем сторонам, \(\displaystyle \angle CBO=\angle BCO= 45^{\circ}{\small .}\) | 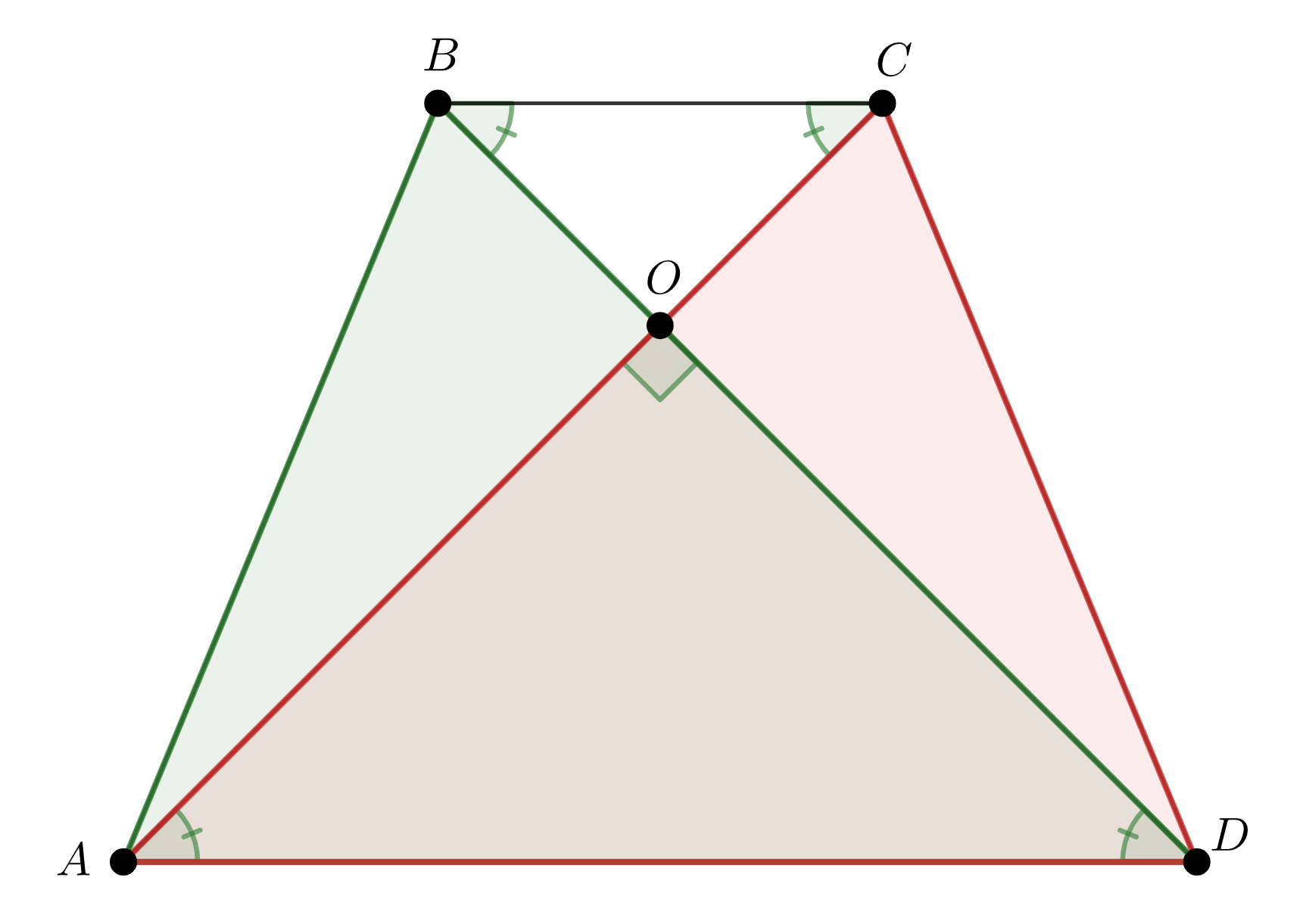 |
Тогда треугольники \(\displaystyle AOD\) и \(\displaystyle BOC\) – прямоугольные, а углы при основаниях равны
\(\displaystyle \angle ADO=\angle DAO=\angle BCO=\angle CBO=45^{\circ}{\small .}\)
Значит, треугольники \(\displaystyle AOD\) и \(\displaystyle BOC\) – равнобедренные.
Через точку \(\displaystyle O\) проведем высоту трапеции, пусть \(\displaystyle K\) и \(\displaystyle H\) – точки ее пересечения с основаниями \(\displaystyle BC\) и \(\displaystyle AD\) соответственно. Следовательно, \(\displaystyle OH\) и \(\displaystyle OK\) – высоты равнобедренных треугольников \(\displaystyle AOD\) и \(\displaystyle BOC{\small ,}\) а значит и медианы, и биссектрисы. Тогда \(\displaystyle AH=HD=\frac{1}{2}\cdot AD{\small ,}\) \(\displaystyle BK=KC=\frac{1}{2}\cdot BC{\small ,}\) \(\displaystyle \angle KOC=\angle KOB=45^{\circ}{\small ,}\) \(\displaystyle \angle HOD=\angle HOA=45^{\circ}{\small .}\) |  |
Рассмотрим треугольники \(\displaystyle KOC\) и \(\displaystyle HOD{\small .}\) Так как \(\displaystyle \angle HOD=\angle HDO=45^{\circ}{\small ,}\) \(\displaystyle \angle KOC=\angle KOB=45^{\circ}{\small ,}\) то треугольники \(\displaystyle KOC\) и \(\displaystyle HOD\) – прямоугольные и равнобедренные, \(\displaystyle OK=KC{\small ,}\) \(\displaystyle OH=HD{\small ,}\) \(\displaystyle KH=OK+OH=KC+HD=\) \(\displaystyle =\frac{BC+AD}{2}=\frac{16}{2}=8{\small .}\) |  |
Второй способ решения
Проведем прямую \(\displaystyle CE\) параллельно прямой \(\displaystyle BD{\small ,}\) точка \(\displaystyle E\) лежит на прямой \(\displaystyle AD{\small .}\) Тогда в четырехугольнике \(\displaystyle BDEC\) прямые \(\displaystyle CE\) и \(\displaystyle BD\) параллельны по построению, прямые \(\displaystyle BC\) и \(\displaystyle DE\) параллельны как прямые, содержащие основания трапеции.
Значит, \(\displaystyle BDEC\) – параллелограмм. По свойству параллелограмма \(\displaystyle DE=BC{\small ,}\) \(\displaystyle CE=BD{\small .}\) Тогда \(\displaystyle AE=AD+DE=AD+BC=16{\small .}\) Отрезки \(\displaystyle AC\) и \(\displaystyle BD\) равны как диагонали равнобедренной трапеции. Следовательно, \(\displaystyle AC=CE{\small .}\) | 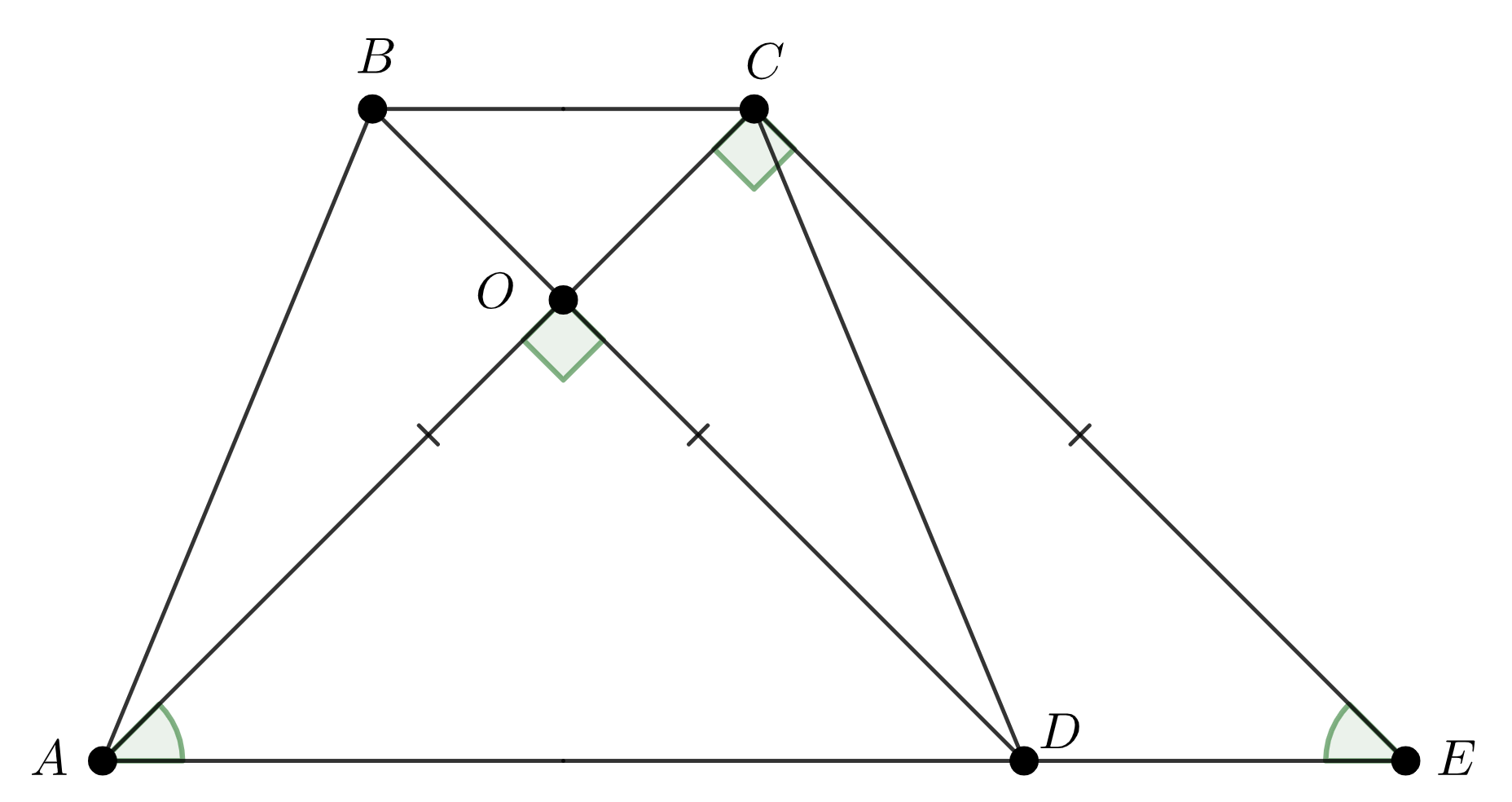 |
Рассмотрим треугольник \(\displaystyle ACE{\small .}\) Углы \(\displaystyle ACE\) и \(\displaystyle AOD\) равны как соответственные углы при пересечении параллельных прямых \(\displaystyle CE\) и \(\displaystyle BD\) секущей \(\displaystyle AC{\small .}\) Значит,
\(\displaystyle \angle ACE =\angle AOD=90^{\circ}{\small .}\)
Следовательно, \(\displaystyle ACE\) – прямоугольный равнобедренный треугольник.
Сумма углов треугольника равна \(\displaystyle 180^{\circ}{\small ,}\) поэтому
\(\displaystyle \angle CAE=\angle CEA = \frac{1}{2} (180^{\circ} - \angle ACE)= \frac{1}{2} (180^{\circ} - 90^{\circ})= \frac{1}{2} \cdot 90^{\circ}=45^{\circ}{\small .}\)
В прямоугольном равнобедренном треугольнике \(\displaystyle ACE\) проведем высоту, медиану и биссектрису \(\displaystyle CN{\small .}\) Так как \(\displaystyle CN\) – медиана, то \(\displaystyle AN=NE=\frac{1}{2}\cdot AE=\frac{1}{2}\cdot 16=8{\small .}\) Так как \(\displaystyle CN\) – биссектриса, то \(\displaystyle \angle ACN=\angle NCE=45^{\circ}=\angle CAN{\small .}\) Тогда треугольник \(\displaystyle ACN\) – прямоугольный равнобедренный, \(\displaystyle CN=AN=8{\small .}\) | 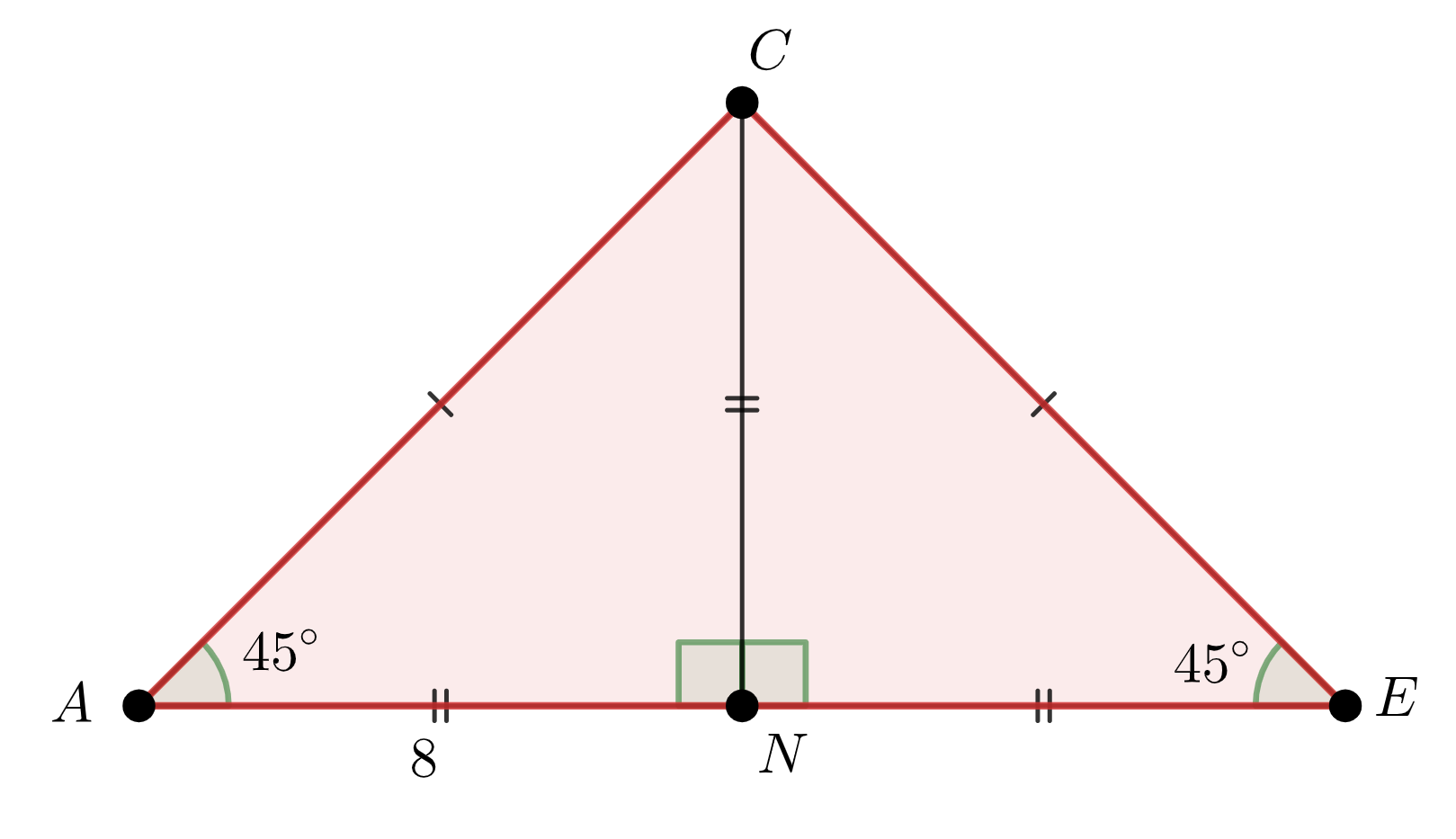 |
Ответ: \(\displaystyle 8{\small .}\)