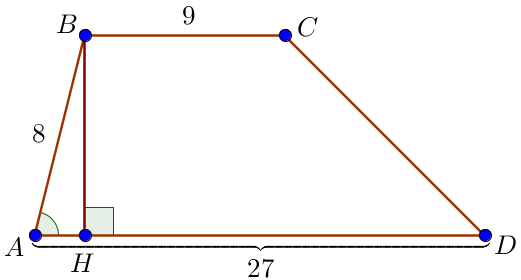
Основания трапеции равны \(\displaystyle 27\) и \(\displaystyle 9\small,\) боковая сторона равна \(\displaystyle 8\small.\) Площадь трапеции равна \(\displaystyle 72\small.\) Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ дайте в градусах.
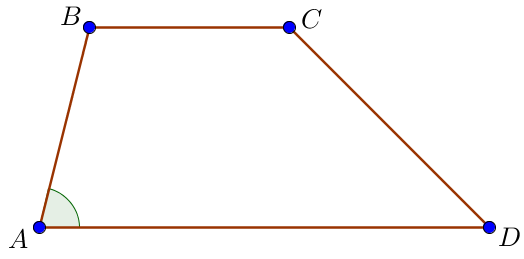
Пусть \(\displaystyle AD=27\) и \(\displaystyle BC=9\) – основания, \(\displaystyle AB=8\) – боковая сторона, \(\displaystyle S_{ABCD}=72\) – площадь трапеции \(\displaystyle ABCD\small.\)
Требуется найти острый угол, прилежащий к стороне \(\displaystyle AB\small.\)
Возможны два случая: угол \(\displaystyle B \) тупой или острый.
По предложенному в условии задачи рисунку угол \(\displaystyle B \) тупой. Тогда надо найти угол \(\displaystyle BAH\small.\) Проведем высоту \(\displaystyle BH \) трапеции. Так как площадь трапеции равна произведению полусуммы оснований на высоту, то \(\displaystyle S_{ABCD}=\frac{AD+BC}{2}\cdot BH\small,\) \(\displaystyle 72=\frac{27+9}{2}\cdot BH\small,\) \(\displaystyle 72={18}\cdot BH\small,\) \(\displaystyle BH=\frac{72}{18}=4\small.\) |
|
Угол \(\displaystyle BAH \) найдем из прямоугольного треугольника \(\displaystyle ABH\small.\) Нам известны катет \(\displaystyle BH=4\) и гипотенуза \(\displaystyle AB=8\small.\) Так как катет в \(\displaystyle 2\) раза меньше гипотенузы, то против этого катета лежит угол \(\displaystyle 30^{\circ}\small.\) Значит, \(\displaystyle \angle BAH =30^{\circ}\small.\) | 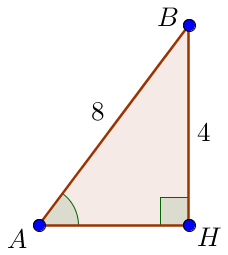 |
Ответ: \(\displaystyle 30^{\circ} \small.\)
Если угол \(\displaystyle B \) острый, то проведем высоту \(\displaystyle AH.\) Тогда требуется найти угол \(\displaystyle ABH.\) Как и выше, \(\displaystyle AH=4. \) | 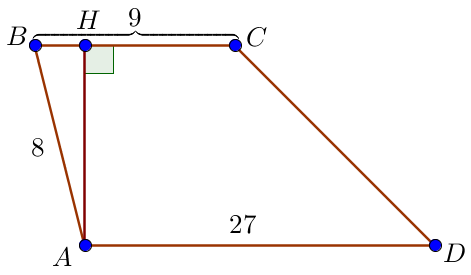 |
Из прямоугольного треугольника \(\displaystyle ABH\) с катетом \(\displaystyle AH=4\) и гипотенузой \(\displaystyle AB=8\) \(\displaystyle \angle ABH =30^{\circ}.\) И в этом случае острый угол, прилежащий к стороне \(\displaystyle AB,\) равен \(\displaystyle 30^{\circ} .\) | 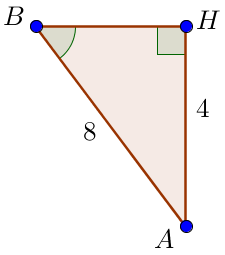 |