Сумма двух углов равнобедренной трапеции равна \(\displaystyle 150^\circ\small{\small .}\) Найдите величину большего угла трапеции. Ответ дайте в градусах.

Пусть \(\displaystyle ABCD\) – равнобедренная трапеция с основаниями \(\displaystyle AD\) и \(\displaystyle BC\small.\)
Воспользуемся свойством равнобедренной трапеции.
Свойство равнобедренной трапеции
Углы при основании равнобедренной трапеции равны.
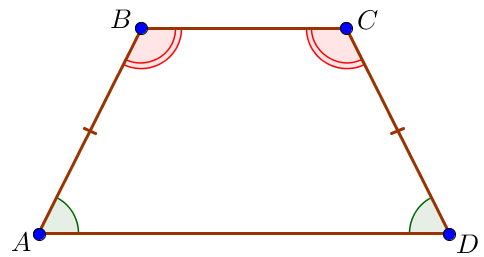
Тогда \(\displaystyle \angle A=\angle D\small,\) \(\displaystyle \angle B=\angle C\small.\)
В условии упоминается пара углов. Это могут быть углы при боковой стороне, углы при основании и противоположные углы. Рассмотрим все варианты.
Сумма углов трапеции при боковой стороне равна \(\displaystyle {180^{\circ}}\small{:}\)
\(\displaystyle \angle A+\angle B=\angle C+\angle D=180^{\circ}\small.\)
Сумма противоположных углов трапеции равна \(\displaystyle {180^{\circ}}\small{:}\)
\(\displaystyle \angle A+\angle C=\angle A+\angle B=180^{\circ}\small,\)
\(\displaystyle \angle D+\angle B=\angle A+\angle B=180^{\circ}\small.\)
Значит, в условии упоминается пара углов при основании: либо при основании \(\displaystyle BC\small,\) либо при основании \(\displaystyle AD\small.\)
При основании \(\displaystyle BC\) углы тупые, \(\displaystyle \angle B=\angle C>90^{\circ}\small,\) откуда
\(\displaystyle \angle B + \angle C>180^{\circ}>150^{\circ}\small.\)
Следовательно, в условии речь идет о смежных углах при основании \(\displaystyle AD{\small: }\)
\(\displaystyle \angle A+\angle D=150^{\circ}\small.\)
Получаем:
\(\displaystyle 2\angle A=150^{\circ}\small,\)
\(\displaystyle \angle A=75^{\circ}\small.\)
Следовательно, наибольший угол трапеции
\(\displaystyle \angle B=180^{\circ}-\angle A=180^{\circ}-75^{\circ}=105^{\circ}\small.\)
Ответ: \(\displaystyle 105^{\circ}\small.\)