На рисунке изображён график функции \(\displaystyle f\left(x\right)=\frac{5}{4}\sqrt{x+b}+c\small.\) Найдите значение \(\displaystyle x\small,\) при котором \(\displaystyle f\left(x\right)=8\small.\)

\(\displaystyle x=\)
Чтобы найти значение \(\displaystyle x\small,\) при котором \(\displaystyle f\left(x\right)=8\small,\)
- найдем неизвестные коэффициенты \(\displaystyle \color{blue}b\) и \(\displaystyle \color{green}c\small,\)
- решим уравнение \(\displaystyle \frac{5}{4} \cdot \sqrt{x+\color{blue}b}+\color{green}c=8\small.\)
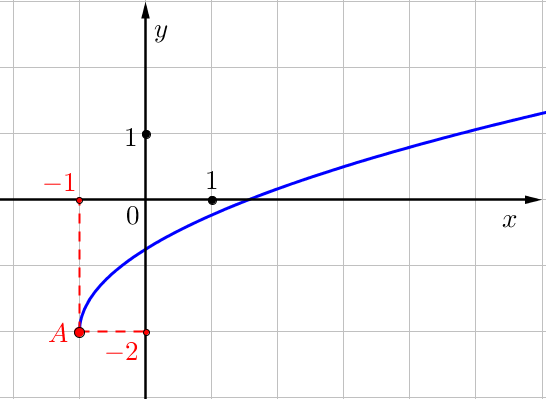
Обозначим отмеченную точку на графике функции \(\displaystyle f\left(x\right)=\frac{5}{4}\sqrt{x+\color{blue}{b}}+\color{green}c\) буквой \(\displaystyle \color{red}A\small.\)
Определим её координаты:
\(\displaystyle x_0=\color{red}{-1}\) – абсцисса, \(\displaystyle y_0=\color{red}{-2}\) – ордината точки \(\displaystyle \color{red}A\small.\)
Найдем значение \(\displaystyle \color{blue}{b}\small.\)
По графику заметим, что абсцисса \(\displaystyle x_0=\color{red}{-1}\) точки \(\displaystyle \color{red}{A} \) равна наименьшему значению переменной \(\displaystyle x\) из области определения функции \(\displaystyle f\left(x\right)=\frac{5}{4}\sqrt{x+\color{blue}{b}}+\color{green}c \small.\)
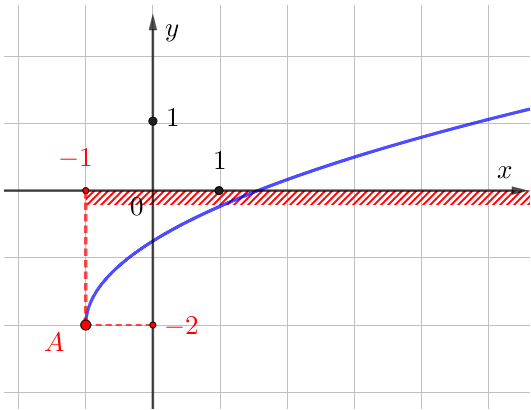
Найдем область определения данной функции.
Воспользуемся правилом:
Корень из числа \(\displaystyle a\) существует (в действительных числах), если \(\displaystyle a\) неотрицательно.
То есть \(\displaystyle \sqrt{a}\) существует, если \(\displaystyle a \geq 0 \small.\)
В нашем случае
\(\displaystyle x+\color{blue}{b} \geq 0\small.\)
Откуда
\(\displaystyle x \geq -\color{blue}b\small.\)
Следовательно, \(\displaystyle x=-\color{blue}b \) – это наименьшее значение переменной в области определения функции.
Значит,
\(\displaystyle -\color{blue}b=\color{red}{-1} \small, \)
\(\displaystyle \color{blue}b=\color{blue}1 \small. \)
Подставим найденное значение \(\displaystyle \color{blue}b,\) получим:
\(\displaystyle f\left(x\right)=\frac{5}{4}\sqrt{x+\color{blue}1}+\color{green}c\small.\)
Найдем значение \(\displaystyle \color{green}c\small.\)
Отметим, что точка \(\displaystyle \color{red}{A(-1;-2)} \) лежит на графике функции \(\displaystyle f\left(x\right)=\frac{5}{4}\sqrt{x+\color{blue}1}+\color{green}c\small.\)
Значит, при подстановке координат \(\displaystyle x=\color{red}{-1}\) и \(\displaystyle y=\color{red}{-2}\) в уравнение \(\displaystyle y=\frac{5}{4}\sqrt{x+\color{blue}1}+\color{green}c\) получим верное равенство.
Таким образом, получаем уравнение:
\(\displaystyle \color{red}{-2}=\frac{5}{4}\sqrt{\color{red}{-1}+\color{blue}1}+\color{green}c\small,\)
откуда
\(\displaystyle \color{green}c=\color{green}{-2} \small.\)
Подставим \(\displaystyle \color{green}c=\color{green}{-2}{:} \)
\(\displaystyle f\left(x\right)=\frac{5}{4}\sqrt{x+\color{blue}{1}}\color{green}{-2}\small.\)
Найдем значение \(\displaystyle x\small,\) при котором \(\displaystyle f\left(x\right)=8\small.\)
Для этого нужно решить уравнение
\(\displaystyle \frac{5}{4}\cdot \sqrt{x+1}-2=8\small.\)
Ответ: \(\displaystyle 63{\small.}\)