Запишем область определения для функции \(\displaystyle f(x)=5\tg x-10x+2{,}5\pi -4{\small.}\)
Так как \(\displaystyle \tg x\) определен только тогда, когда \(\displaystyle x\,\cancel{=}\,\frac{\pi}{2}+\pi m{\small,}\,\,m\in\mathbb{Z}{\small,}\) то область определения имеет вид
\(\displaystyle x\,\cancel{=}\,\frac{\pi}{2}+\pi m{\small.}\)
1) Найдем производную функции \(\displaystyle f(x)=5\tg x-10x+2{,}5\pi -4{\small.}\)
\(\displaystyle f^{\prime}(x)=\left(5\text{tg} x-10x+2{,}5\pi -4\right)^{\prime}=\frac{5}{\cos^2 x}-10{\small.}\)
\(\displaystyle \begin{aligned}(5\tg x-10x+2{,}5\pi -4)^{\prime}=(5\tg x)^{\prime}-(10x)^{\prime}+(2{,}5\pi)^{\prime}-(4)^{\prime}=5(\tg x)^{\prime}-10(x)^{\prime}+0-0=\\[5px]=5\cdot\frac{1}{\cos^2 x}-10\cdot1=\frac{5}{\cos^2 x}-10{\small.}\end{aligned}\)
Перепишем \(\displaystyle f^{\prime}(x)=\frac{5}{\cos^2 x}-10\) в виде дроби:
\(\displaystyle \frac{5}{\cos^2 x}-10=\frac{5-10\cos^2 x}{\cos^2 x}{\small.}\)
2) Найдем корни числителя и знаменателя \(\displaystyle f^{\prime}(x)=\frac{5-10\cos^2 x}{\cos^2 x}{\small.}\)
\(\displaystyle x_1=\frac{\pi}{4}+2\pi n_1{\small,}\) \(\displaystyle x_2=\frac{3\pi}{4}+2\pi n_2{\small,}\) \(\displaystyle x_3=-\frac{\pi}{4}+2\pi n_3{\small,}\) \(\displaystyle x_4=-\frac{3\pi}{4}+2\pi n_4{\small,}\) где \(\displaystyle n_1{\small,}\,n_2{\small,}\,n_3{\small,}\,n_4 \in \mathbb{Z}\) корни числителя \(\displaystyle f^{\prime}(x){\small.}\)
Приравняем числитель \(\displaystyle \frac{5-10\cos^2 x}{\cos^2 x}\) к нулю:
\(\displaystyle 5-10\cos^2 x=0{\small,}\)
\(\displaystyle 5=10\cos^2 x{\small,}\)
\(\displaystyle \cos^2 x=\frac{1}{2}{\small,}\) значит, \(\displaystyle \cos x =\sqrt{\frac{1}{2}}\) или \(\displaystyle \cos x=-\sqrt{\frac{1}{2}}\)
Приведем иррациональное выражение \(\displaystyle \sqrt{\frac{1}{2}}\) к дроби с рациональным знаменателем:
\(\displaystyle \sqrt{\frac{1}{2}}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{\sqrt{2}\cdot{\sqrt{2}}}=\frac{\sqrt{2}}{2}{\small.}\)
Получаем уравнения \(\displaystyle \cos x = \frac{\sqrt{2}}{2}\) и \(\displaystyle \cos x = -\frac{\sqrt{2}}{2}{\small.}\)
Решим эти уравнения.
Поскольку значения косинуса лежат на оси \(\displaystyle \rm OX{\small,}\) то пересечем тригонометрическую окружность c прямыми \(\displaystyle x=\frac{\sqrt{2}}{2}\) и \(\displaystyle x=-\frac{\sqrt{2}}{2}{\small.}\)
| Пересекаем окружность прямой \(\displaystyle x=\frac{\sqrt{2}}{2}\) | Пересекаем окружность прямой \(\displaystyle x=-\frac{\sqrt{2}}{2}\) |
Так как \(\displaystyle \cos \frac{\pi}{4}=\frac{\sqrt{2}}{2}{\small,}\) то зеленый угол равен \(\displaystyle \color{green}{\frac{\pi}{4}}{\small,}\) а синий по симметричности \(\displaystyle \color{blue}{-\frac{\pi}{4}}{\small:}\) 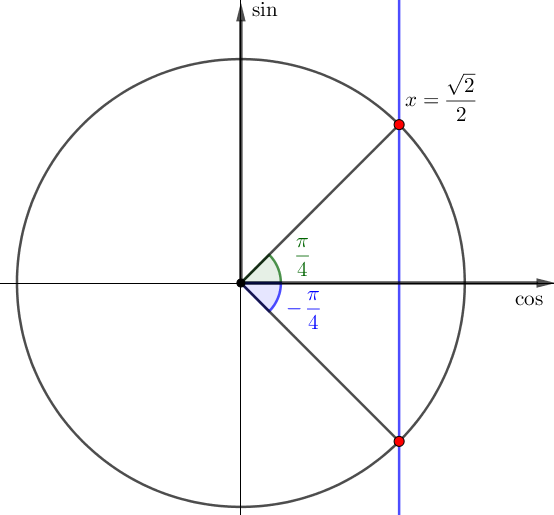
| Красный угол равен \(\displaystyle \pi-\color{green}{\frac{\pi}{4}}=\color{red}{\frac{3\pi}{4}}{\small,}\) а фиолетовый по симметричности \(\displaystyle \color{Purple}{-\frac{3\pi}{4}}{\small:}\) 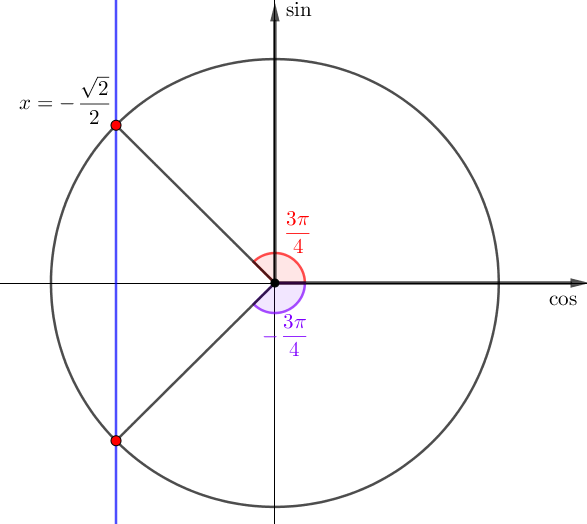
|
Получаем четыре набора решений:
 | - \(\displaystyle x_1=\frac{\pi}{4}+2\pi n_1{\small,}\)
- \(\displaystyle x_2=\frac{3\pi}{4}+2\pi n_2{\small,}\)
- \(\displaystyle x_3=-\frac{\pi}{4}+2\pi n_3{\small,}\)
- \(\displaystyle x_4=-\frac{3\pi}{4}+2\pi n_4{\small,}\)
где \(\displaystyle n_1{\small,}\,n_2{\small,}\,n_3{\small,}\,n_4 \in \mathbb{Z}\) |
\(\displaystyle x_5=\frac{\pi}{2}+2\pi k{\small,}\,\, k \in \mathbb{Z}\) и \(\displaystyle x_6=-\frac{\pi}{2}+2\pi l{\small,}\,\, l \in \mathbb{Z}\) корни знаменателя \(\displaystyle f^{\prime}(x){\small.}\)
Приравняем знаменатель \(\displaystyle \frac{5-10\cos^2 x}{\cos^2 x}\) к нулю:
\(\displaystyle \cos^2 x=0{\small,}\) значит, \(\displaystyle \cos x =0{\small.}\)
Решим элементарное тригонометрическое уравнение \(\displaystyle \cos x = 0{\small.}\)
Поскольку значения косинуса лежат на оси \(\displaystyle \rm OX{\small,}\) то пересечем прямую \(\displaystyle x=0\) и тригонометрическую окружность.

Получаем два набора решений:
 |  |
| \(\displaystyle x_5=\frac{\pi}{2}+2\pi k{\small,}\,\, k \in \mathbb{Z}\) | \(\displaystyle x_6=-\frac{\pi}{2}+2\pi l{\small,}\,\, l \in \mathbb{Z}\) |
3) Из корней числителя и знаменателя \(\displaystyle f^{\prime}(x)\) выберем корни, лежащие на отрезке \(\displaystyle \left[-\frac{\pi}{3};\frac{\pi }{3}\right]{\small.}\)
\(\displaystyle x=\frac{\pi}{4}\) и \(\displaystyle x=-\frac{\pi}{4}\) корни, лежащие на отрезке \(\displaystyle \text{\LARGE [}-\frac{\pi}{3};\frac{\pi }{3}\text{\LARGE ]}{\small.}\)
Построим тригонометрическую окружность. На ней отметим точки, соответствующие корням числителя и знаменателя \(\displaystyle f^{\prime}(x){\small:}\)
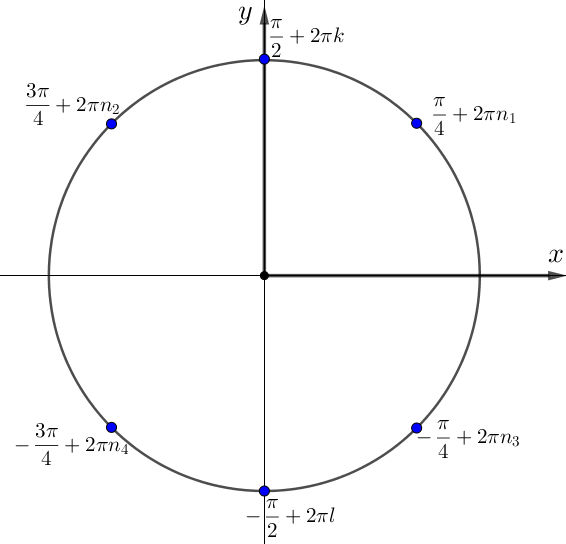
Отметим на единичной окружности отрезок \(\displaystyle \left[-\frac{\pi}{3};\frac{\pi }{3}\right]{\small,}\) получаем:
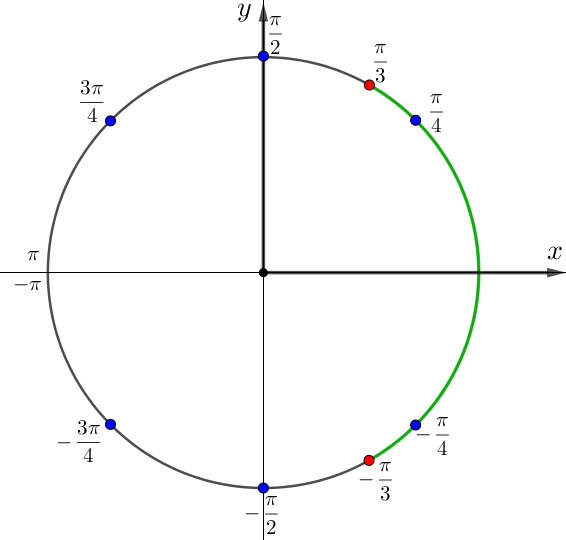
Значит, на отрезке \(\displaystyle \left[-\frac{\pi}{3};\frac{\pi }{3}\right]\) лежат два корня \(\displaystyle x=\frac{\pi}{4}\) и \(\displaystyle x=-\frac{\pi}{4}{\small.}\)
4) Отметим на числовой прямой корни числителя и знаменателя производной. Учитывая область определения функции \(\displaystyle f(x){\small,}\) получаем:

Так как требуется найти наименьшее значение функции на отрезке \(\displaystyle \left[-\frac{\pi}{3};\frac{\pi }{3}\right]{\small ,}\) то получаем:

Найдем знаки производной на интервалах \(\displaystyle \left(-\frac{\pi}{2};\,-\frac{\pi}{4}\right){\small,}\) \(\displaystyle \left(-\frac{\pi}{4};\,\frac{\pi}{4}\right)\) и \(\displaystyle \left(\frac{\pi}{4};\, \frac{\pi}{2}\right){\small.}\)
- на интервалах \(\displaystyle \color{green}{\left(-\frac{\pi}{2};\,-\frac{\pi}{4}\right)}\) и \(\displaystyle \color{blue}{\left(\frac{\pi}{4};\, \frac{\pi}{2}\right)}\) функция \(\displaystyle f^{\prime}(x)>0{\small,}\)
- на интервале \(\displaystyle \color{Purple}{\left(-\frac{\pi}{4};\,\frac{\pi}{4}\right)}\) функция \(\displaystyle f^{\prime}(x)<0{\small.}\)
Определим знак функции \(\displaystyle f^{\prime}(x)=\frac{5-10\cos^2 x}{\cos^2 x}\) на каждом из интервалов:
\(\displaystyle \color{green}{\left(-\frac{\pi}{2};\,-\frac{\pi}{4}\right)}{\small,}\) \(\displaystyle \color{Purple}{\left(-\frac{\pi}{4};\,\frac{\pi}{4}\right)}{\small,}\) \(\displaystyle \color{blue}{\left(\frac{\pi}{4};\, \frac{\pi}{2}\right)}{\small.}\)
Для этого выберем по точке на каждом из интервалов и определим в этой точке знак функции. Получаем:
- для \(\displaystyle \color{green}{x=-\frac{\pi}{3} \in \left(-\frac{\pi}{2};\,-\frac{\pi}{4}\right)}\) знак
\(\displaystyle f^{\prime}\left(\color{green}{-\frac{\pi}{3}}\right)=\frac{5-10\cos^2 \left(-\frac{\pi}{3}\right)}{\cos^2 \left(-\frac{\pi}{3}\right)}=\frac{5-10\cos^2 \left(\frac{\pi}{3}\right)}{\cos^2 \left(\frac{\pi}{3}\right)}=\frac{5-10\cdot\frac{1}{4}}{\frac{1}{4}}=10\color{red}{>}0{\small ;}\)
для \(\displaystyle \color{Purple}{x=0 \in \left(-\frac{\pi}{4};\,\frac{\pi}{4}\right)}\) знак \(\displaystyle f^{\prime}(\color{Purple}{0})=\frac{5-10\cos^2 0}{\cos^2 0}=\frac{5-10\cdot1}{1}=-5\color{red}{<}0{\small;}\)
- для \(\displaystyle \color{blue}{x=\frac{\pi}{3} \in{\left(\frac{\pi}{4};\, \frac{\pi}{2}\right)}}\) знак \(\displaystyle f^{\prime}\left(\color{blue}{\frac{\pi}{3}}\right)=\frac{5-10\cos^2 \left(\frac{\pi}{3}\right)}{\cos^2 \left(\frac{\pi}{3}\right)}=\frac{5-10\cdot\frac{1}{4}}{\frac{1}{4}}=10\color{red}{>}0{\small .}\)
Значит,
- на интервалах \(\displaystyle \color{green}{\left(-\frac{\pi}{2};\,-\frac{\pi}{4}\right)}\) и \(\displaystyle \color{blue}{\left(\frac{\pi}{4};\, \frac{\pi}{2}\right)}\) функция \(\displaystyle f^{\prime}(x)>0{\small,}\)
- на интервале \(\displaystyle \color{Purple}{\left(-\frac{\pi}{4};\,\frac{\pi}{4}\right)}\) функция \(\displaystyle f^{\prime}(x)<0{\small.}\)
Отмечая знаки производной на картинке, получаем:
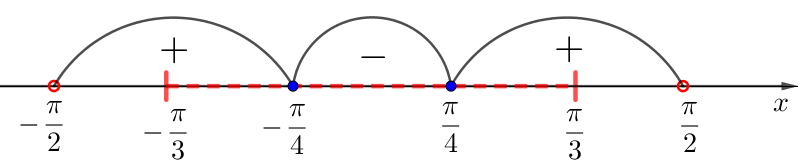
Значит, и на интервалах \(\displaystyle {\left(-\frac{\pi}{3};\,-\frac{\pi}{4}\right)}\) и \(\displaystyle {\left(\frac{\pi}{4};\, \frac{\pi}{3}\right)}\) производная положительна:
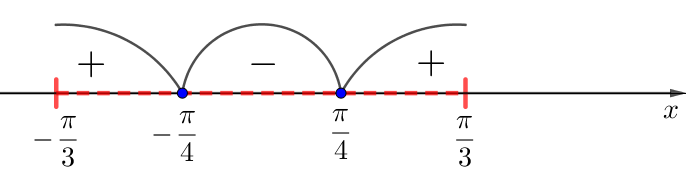
5) Определим промежутки возрастания и убывания функции \(\displaystyle f(x)=5\tg x-10x+2{,}5\pi -4{\small ,}\) пользуясь правилом.
ПравилоЕсли для любой точки \(\displaystyle x_0\in(a;\,b)\) производная \(\displaystyle f^{\prime}(x_0)\) существует и \(\displaystyle f^{\prime}(x_0)>0{\small,}\) то
функция \(\displaystyle f(x)\) возрастает \(\displaystyle \nearrow\) на всем интервале \(\displaystyle (a;\,b){\small.}\)
Если для любой точки \(\displaystyle x_0\in(a;\,b)\) производная \(\displaystyle f^{\prime}(x_0)\) существует и \(\displaystyle f^{\prime}(x_0)<0{\small,}\) то
функция \(\displaystyle f(x)\) убывает \(\displaystyle \searrow\) на всем интервале \(\displaystyle (a;\,b){\small.}\)
Зная знаки производной \(\displaystyle f^{\prime}(x){\small,}\) определим промежутки возрастания и убывания \(\displaystyle f(x){\small:}\)
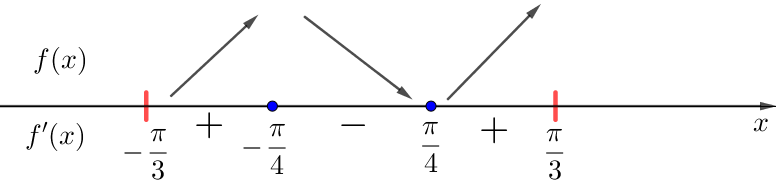
6) Схематично изобразим график (f(x)\) на отрезке \(\displaystyle \left[-\frac{\pi}{3};\,\frac{\pi }{3} \right]{\small:}\)
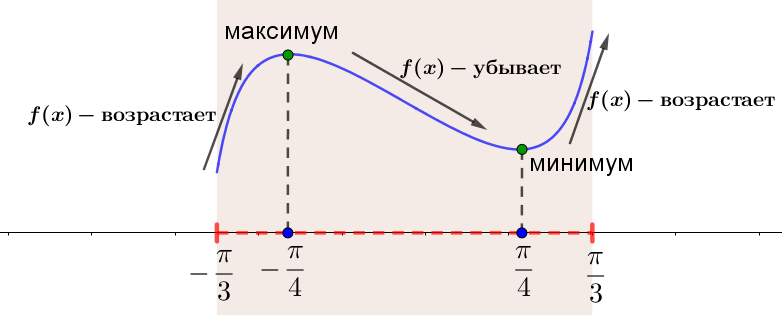
Видно, что на отрезке \(\displaystyle \left[-\frac{\pi}{3};\,\frac{\pi }{3} \right]\) функция достигает наименьшего значения либо в точке минимума \(\displaystyle \color{green}{x=\frac{\pi}{4}}{\small,}\) либо на левом конце в точке \(\displaystyle \color{blue}{x=-\frac{\pi}{3}}{\small.}\)
Вычислим значения в этих точках и сравним:
\(\displaystyle f\left(\color{green}{\frac{\pi}{4}}\right)=5\tg \frac{\pi}{4}-10\cdot\frac{\pi}{4}+2{,}5\pi -4=5\cdot1-\cancel{2{,}5\pi}+\cancel{2{,}5\pi}-4=\color{green}{1}{\small,}\)
\(\displaystyle f\left(\color{blue}{-\frac{\pi}{3}}\right)=5\tg \left(-\frac{\pi}{3}\right)-10\cdot\left(-\frac{\pi}{3}\right)+2{,}5\pi -4=\color{blue}{5\tg \left(-\frac{\pi}{3}\right)+\frac{35\pi}{6}-4}{\small.}\)
Используя формулы приведения и таблицу значений тангенса, вычислим \(\displaystyle \tg \left(-\frac{\pi}{3}\right){\small:}\)
\(\displaystyle \tg \left(-\frac{\pi}{3}\right)=-\tg \left(\frac{\pi}{3}\right)=-\sqrt{3}{\small.}\)
Значит, \(\displaystyle f\left(\color{blue}{-\frac{\pi}{3}}\right)=\color{blue}{5\tg \left(-\frac{\pi}{3}\right)+\frac{35\pi}{6}-4}=\color{blue}{-5\sqrt{3}+\frac{35\pi}{6}-4}{\small.}\)
Так как \(\displaystyle \pi>3\) и \(\displaystyle \sqrt{3}<2{\small,}\) получаем:
\(\displaystyle \color{blue}{-5\sqrt{3}+\frac{35\pi}{6}-4}>-5\cdot2+\frac{35\cdot3}{6}-4=\frac{7}{2}=3{,}5>\color{green}{1}{\small.}\)
То есть \(\displaystyle f\left(\color{green}{\frac{\pi}{4}}\right)<f\left(\color{blue}{-\frac{\pi}{3}}\right){\small.}\)
Таким образом, наименьшее значение достигается в точке \(\displaystyle \color{green}{x=\frac{\pi}{4}}\) и оно равно \(\displaystyle {f\left(\color{green}{\frac{\pi}{4}}\right)}=\color{green}{1}{\small.}\)
Ответ: \(\displaystyle 1{\small.}\)