Skip to main content

Теория: Разложение на множители. Графический метод

Задание

Найдите все значения \(\displaystyle a {\small ,}\) при каждом из которых система уравнений

\(\displaystyle \begin{cases}&\kern{-1em} \left( xy^2-2xy-6y+12\right) \sqrt{6-x}=0{\small ,}\\&\kern{-1em}y=ax\end{cases} \)

имеет ровно три различных решения.

Решение

Решим систему графическим методом. Для этого:

  1. Построим график первого уравнения системы (данное уравнение не содержит параметр \(\displaystyle a\)). 
  2. Проанализируем, как выглядит график второго уравнения в зависимости от параметра.
  3. Найдём, при каком значении параметра \(\displaystyle a\) построенные графики имеют ровно три точки пересечения.

 

Шаг 1. Построим график первого уравнения системы. 

Рассмотрим уравнение \(\displaystyle \left( xy^2-2xy-6y+12\right) \sqrt{6-x}=0{\small .}\)

Найдем область определения данного уравнения

\(\displaystyle 6-x \geqslant0\) или \(\displaystyle x \leqslant 6{\small .}\)

Значит, все решения уравнения расположены левее вертикальной прямой \(\displaystyle x=6\) или на данной прямой.

Для построения графика упростим левую часть уравнения. 

Заметим, что выражение в скобках раскладывается на множители очевидным образом:

\(\displaystyle \left( xy(y-2)-6(y-2)\right) \sqrt{6-x}=0{\small ,}\)

\(\displaystyle (y-2)(xy-6) \sqrt{6-x}=0{\small .}\)

Заметим, что выражение \(\displaystyle xy^2-2xy-6y+12\) может быть разложено на множители, если его рассматривать как квадратное относительно \(\displaystyle y{\small .}\) 

Таким образом, исходное уравнение распадается на три уравнения: 

  1. \(\displaystyle y-2=0{\small ,}\) откуда \(\displaystyle y=2{\small .}\) Графиком является горизонтальная прямая, проходящая через точку \(\displaystyle (0;\,2){\small .}\)
  2. \(\displaystyle xy-6=0{\small ,}\) откуда \(\displaystyle y=\frac{6}{x}{\small .}\) Данное уравнение задаёт гиперболу.
  3. \(\displaystyle \sqrt{6-x}=0{\small .}\) Решение уравнения \(\displaystyle x=6{\small ,}\) а графиком является вертикальная прямая, проходящая через точку \(\displaystyle (6;\,0){\small .}\)

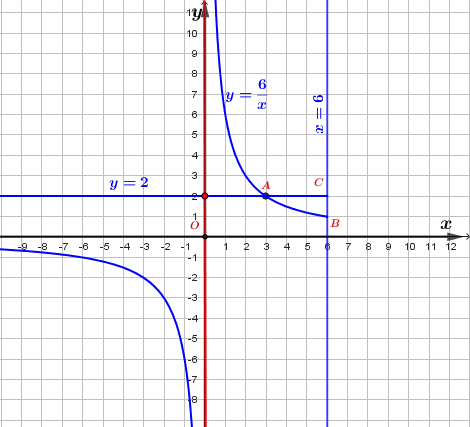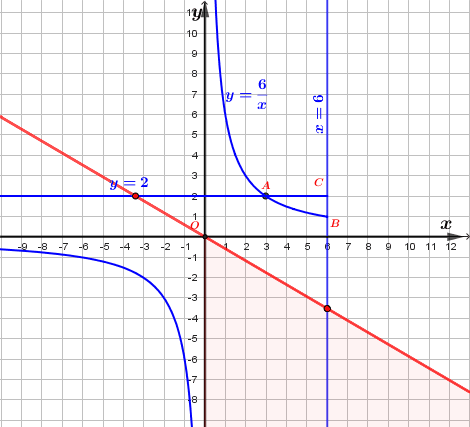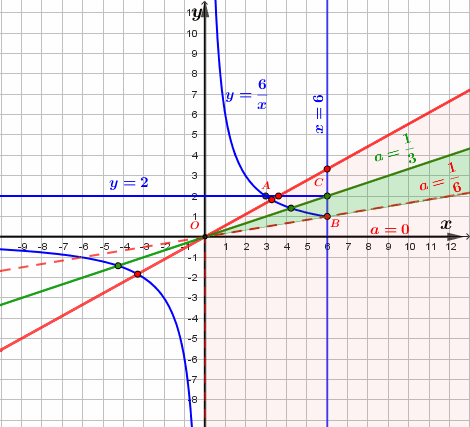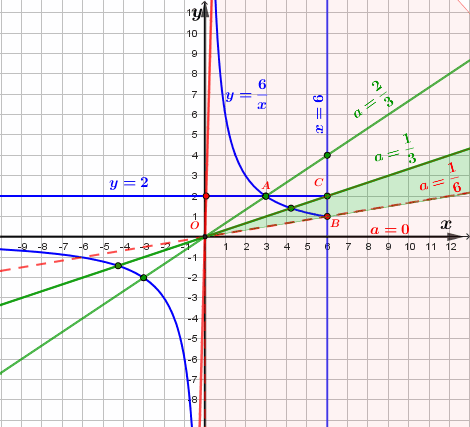
Найдём точки пересечения графиков.

Гипербола \(\displaystyle y=\frac{6}{x}\) пересекает прямые \(\displaystyle y=2\) и \(\displaystyle x=6\) в точках \(\displaystyle A(3;2)\) и \(\displaystyle B(6;1){\small .}\)

Прямые \(\displaystyle y=2\) и \(\displaystyle x=6 \) пересекаются в точке \(\displaystyle C(6;2){\small .}\)

Изобразим все три графика, учитывая ограничение \(\displaystyle x \leqslant 6{\small .}\)

 

Шаг 2. Проанализируем, как выглядит график второго уравнения в зависимости от параметра.

Рассмотрим второе уравнение исходной системы \(\displaystyle y=ax{\small .}\)

Это уравнение прямой с угловым коэффициентом \(\displaystyle a{\small .}\)

Поскольку при \(\displaystyle x=\red0 \) получаем \(\displaystyle y=a\cdot \red0=\blue0{ \small ,} \) то данная прямая всегда проходит через точку начала координат \(\displaystyle O(\red0;\blue0){\small .}\)

Значит, при различных значениях \(\displaystyle a\) будем иметь разные прямые, проходящие через точку \(\displaystyle O(0;0){\small .}\)

 

Шаг 3. Найдём, при каких значениях параметра \(\displaystyle a\) построенные графики имеют ровно три точки пересечения.

Будем поворачивать прямую \(\displaystyle y=ax\) от нижнего вертикального положения до верхнего против часовой стрелки и считать количество точек пересечения прямой с графиком первого уравнения исходной системы.

Получаем:

  • ниже оси \(\displaystyle Ox\) (соответствует \(\displaystyle a<0\))  – \(\displaystyle 2\) точки;
  • при совпадении с \(\displaystyle Ox\) (\(\displaystyle a=0\)) – \(\displaystyle 1\) точка;
  • от оси \(\displaystyle Ox\) до прямой \(\displaystyle OB\) включительно – \(\displaystyle 2\) точки;
  • от \(\displaystyle OB\) (не включая) до \(\displaystyle OC\) включительно – \(\displaystyle \color{green}{3}\) точки;
  • от \(\displaystyle OC\) до \(\displaystyle OA\) – \(\displaystyle 4\) точки;
  • при совпадении с \(\displaystyle OA\) – \(\displaystyle \color{green}{3}\) точки;
  • выше \(\displaystyle OA\) – \(\displaystyle 4\) точки.

 

Определим, при каких значениях \(\displaystyle a\) прямая \(\displaystyle y=ax\) проходит через точки \(\displaystyle A{ \small ,}\,B\) и \(\displaystyle C{\small :}\) 

  • через \(\displaystyle B\) при \(\displaystyle a=\frac{1}{6}{ \small ,}\) 

  • через \(\displaystyle C\) при \(\displaystyle a=\frac{1}{3}{\small ,}\)

  • через точку \(\displaystyle A\) при \(\displaystyle a=\frac{2}{3}{ \small .}\)

Значит,

  • сектору от \(\displaystyle OB\) до \(\displaystyle OC\) включительно соответствует \(\displaystyle \frac{1}{6} < a \le \frac{1}{3}{\small ,}\) 
  • прямой \(\displaystyle OB\) – \(\displaystyle a=\frac{2}{3}{ \small .}\)

Таким образом, исходная система имеет ровно три решения при \(\displaystyle \frac{1}{6} < a \le \frac{1}{3}{\small ,}\) \(\displaystyle a=\frac{2}{3}{ \small .}\)

Ответ:  \(\displaystyle \frac{1}{6} < a \le \frac{1}{3}{\small ,}\) \(\displaystyle a=\frac{2}{3}{ \small .}\)