Решим систему графическим методом. Для этого:
- Построим график первого уравнения системы (данное уравнение не содержит параметр \(\displaystyle a\)).
- Проанализируем, как выглядит график второго уравнения в зависимости от параметра \(\displaystyle a{\small .}\)
- Найдем, при каких значениях параметра \(\displaystyle a\) построенные графики имеют ровно две точки пересечения.
Шаг 1. Строим график первого уравнения системы.
Раскроем модуль. Получим две системы:\(\displaystyle \begin{cases}&\kern{-1em} x-5y+5 \geqslant 0{\small ,}\\&\kern{-1em}x^2+4x+y^2+4y=57\end{cases} \) или \(\displaystyle \begin{cases}&\kern{-1em} x-5y+5 < 0{\small ,}\\&\kern{-1em}x^2+6x+y^2-6y=47 {\small .}\end{cases} \)
\(\displaystyle \begin{cases} &\kern{-1em} x-5y+5 \geqslant 0{\small ,}\\ &\kern{-1em}x^2+5x+y^2-y-(x-5y+5)=52 \end{cases} \) | или | \(\displaystyle \begin{cases} &\kern{-1em} x-5y+5 <0{\small ,}\\ &\kern{-1em}x^2+5x+y^2-y+(x-5y+5)=52 {\small ;} \end{cases} \) |
\(\displaystyle \begin{cases} &\kern{-1em} x-5y+5 \geqslant 0{\small ,}\\ &\kern{-1em}x^2+5x+y^2-y-x+5y-5=52 \end{cases} \) | или | \(\displaystyle \begin{cases} &\kern{-1em} x-5y+5 <0{\small ,}\\ &\kern{-1em}x^2+5x+y^2-y+x-5y+5=52 {\small ;} \end{cases} \) |
| \(\displaystyle \begin{cases} &\kern{-1em} x-5y+5 \geqslant 0{\small ,}\\[10px] &\kern{-1em}x^2+4x+y^2+4y=57 \end{cases} \) | или | \(\displaystyle \begin{cases} &\kern{-1em} x-5y+5 <0{\small ,}\\[10px] &\kern{-1em}x^2+6x+y^2-6y=47 {\small .} \end{cases} \) |
Переписывая неравенства и выделяя полный квадрат в уравнениях систем, получаем:\(\displaystyle \begin{cases}&\kern{-1em} y \leqslant \dfrac{1}{5}x+1{\small ,}\\&\kern{-1em}(x+2)^2+(y+2)^2=65\end{cases} \) или \(\displaystyle \begin{cases}&\kern{-1em} y > \dfrac{1}{5}x+1{\small ,}\\&\kern{-1em}(x+3)^2+(y-3)^2=65 {\small .}\end{cases} \)
Дополним вторые уравнения систем до полных квадратов:
\(\displaystyle x^2+4x+y^2+4y=57{\small ,}\) \(\displaystyle x^2+4x\red{+4}+y^2+4y\blue{+4}\red{-4}\blue{-4}=57 {\small ,}\) \(\displaystyle (x+2)^2+(y+2)^2=65{\small .}\) | \(\displaystyle x^2+6x+y^2-6y=47{\small .}\) \(\displaystyle x^2+6x\red{+9}+y^2-6y\blue{+9}\red{-9}\blue{-9}=47 {\small ,}\) \(\displaystyle (x+3)^2+(y-3)^2=65{\small .}\) |
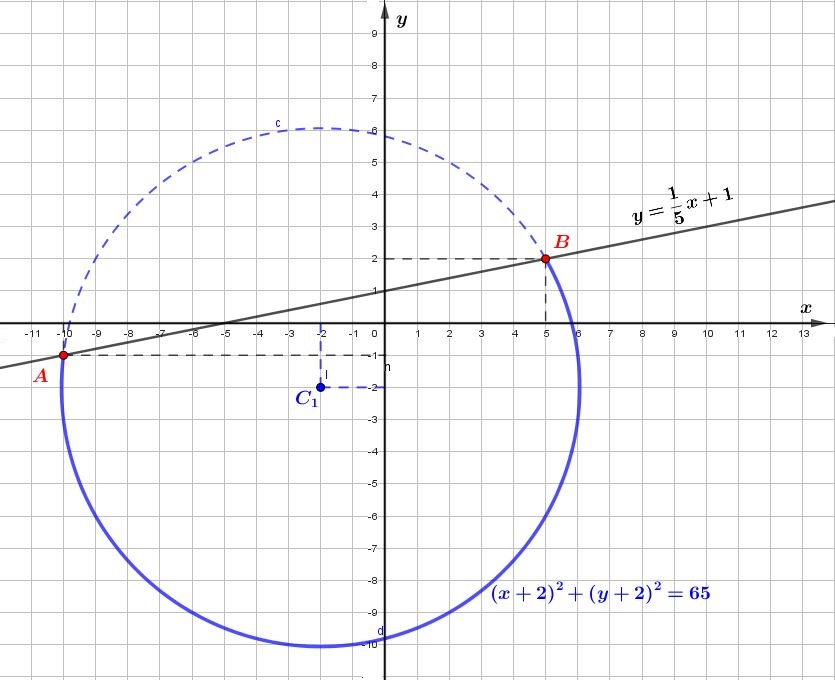
Решениями первой системы являются точки окружности с центром \(\displaystyle C_{1}(-2;-2)\) и радиусом \(\displaystyle \sqrt{65}{\small ,}\) расположенные не выше прямой \(\displaystyle y =\frac{1}{5}x+1{\small .}\)
Решения второй системы – точки окружности с центром \(\displaystyle C_{2}(-3;3)\) и радиусом \(\displaystyle \sqrt{65}{\small ,}\) лежащие выше прямой \(\displaystyle y =\frac{1}{5}x+1{\small .}\)
Обе системы получены из исходного уравнения \(\displaystyle x^2+5x+y^2-y-\left|x-5y+5\right|=52\) при \(\displaystyle x-5y+5\geqslant 0\) либо при \(\displaystyle x-5y+5 <0{\small :}\)\(\displaystyle \begin{cases}&\kern{-1em} x-5y+5 \geqslant 0{\small ,}\\&\kern{-1em}x^2+5x+y^2-y-(x-5y+5)=52 \end{cases} \) или \(\displaystyle \begin{cases}&\kern{-1em} x-5y+5 <0{\small ,}\\&\kern{-1em}x^2+5x+y^2-y+(x-5y+5)=52 {\small .}\end{cases} \)
Значит, при \(\displaystyle x-5y+5 =0\) или \(\displaystyle y =\frac{1}{5}x+1\) вторые уравнения систем превращаются в одно и то же уравнение:
\(\displaystyle x^2+5x+y^2-y=52{\small .} \)
Подставим \(\displaystyle y =\frac{1}{5}x+1\) и найдем точки пересечения окружностей с прямой:
\(\displaystyle A(-10;-1)\) и \(\displaystyle B(5;2){\small .}\)
Подставляя \(\displaystyle y =\frac{1}{5}x+1\) или \(\displaystyle x =5y-5\) в уравнение \(\displaystyle x^2+5x+y^2-y=52{\small ,} \) получаем:
\(\displaystyle (5y-5)^2+5\cdot (5y-5)+y^2-y=52{\small .} \)
Раскроем скобки и решим квадратное уравнение:
\(\displaystyle 25y^2-50y+25+25y-25+y^2-y-52=0{\small ,}\)
\(\displaystyle 26y^2-26y-52=0\,\color{red}{\bigg| : 13}\)
\(\displaystyle y^2-y-2=0{\small .}\)
\(\displaystyle {\rm D}=1^2-4 \cdot 1\cdot (-2)=9{\small ,}\) \(\displaystyle {\sqrt {\rm D}} =3{\small .}\)
\(\displaystyle y_{1}=\frac {1+3}{2}=2{\small ,} \,\, y_{2}=\frac {1-3}{2}=-1{\small .}\)
Тогда
\(\displaystyle x_{1}=5y-5=5\cdot2-5=5{\small ,}\) \(\displaystyle x_{2}=5\cdot(-1)-5=-10{\small .}\)
Значит, точки пересечения имеют координаты \(\displaystyle (5;2)\) и \(\displaystyle (-10;-1){\small .}\)
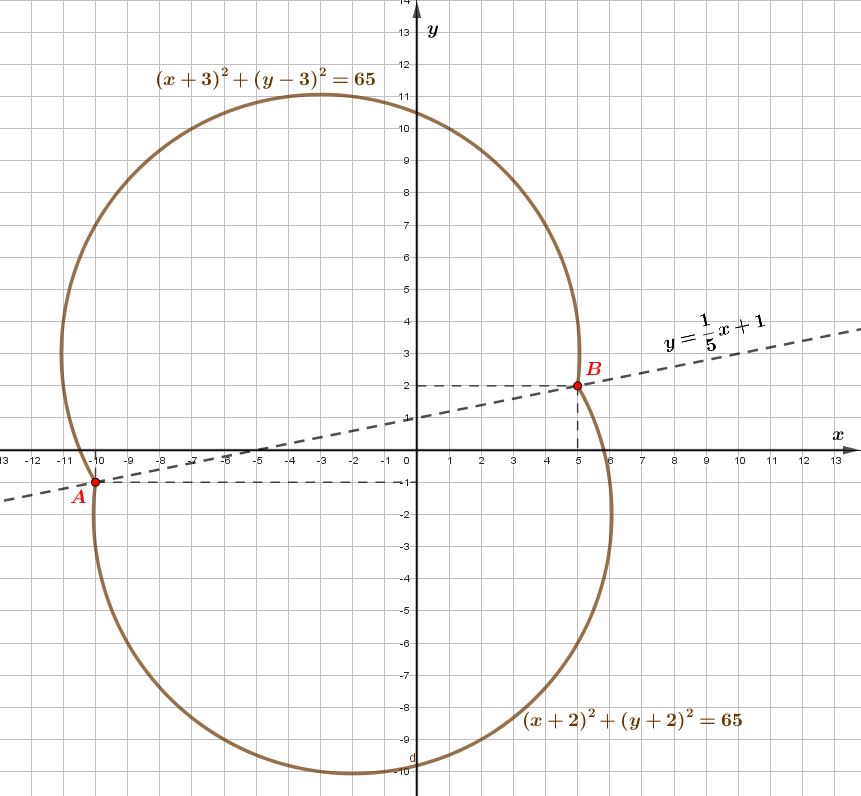
Построим графики каждой из систем и объединим их. Получим график уравнения\(\displaystyle x^2+5x+y^2-y-\left|x-5y+5\right|=52{\small .}\)
Построим графики для каждой из систем:
 | или | 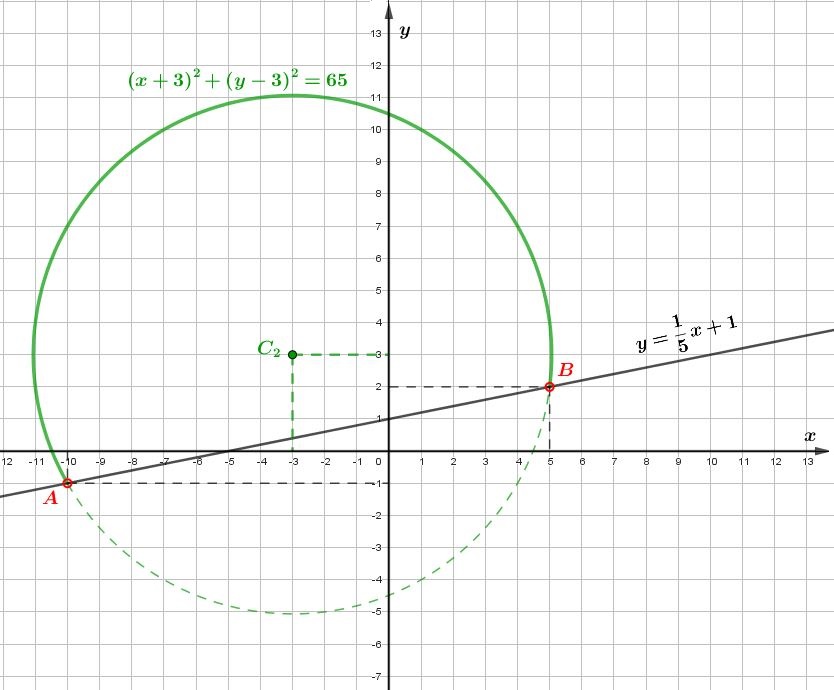 |
Шаг 2. Проанализируем, как выглядит график второго уравнения в зависимости от параметра \(\displaystyle a{\small .}\)
Рассмотрим второе уравнение исходной системы \(\displaystyle y-2=a(x-5){\small .}\)
Это уравнение прямой \(\displaystyle y=a(x-\red5)+\blue2\) с угловым коэффициентом \(\displaystyle a{\small .}\)
Поскольку при \(\displaystyle x=\red5 \) получаем \(\displaystyle y=a\cdot 0+2=\blue2{ \small ,} \) то эта прямая всегда проходит через точку \(\displaystyle (\red5;\blue2){\small .}\)
Значит, при различных значениях \(\displaystyle a\) будем иметь разные прямые, проходящие через точку \(\displaystyle B(5;2){\small .}\)
Шаг 3. Найдём, при каких значениях параметра \(\displaystyle a\) построенные графики имеют ровно две точки пересечения.
Посмотрим, в каких случаях прямая \(\displaystyle y=a(x-5)+2\) имеет с графиком первого уравнения \(\displaystyle 2\) точки пересечения.
Ровно две точки получается в двух случаях:
При повороте прямой \(\displaystyle y=a(x-5)+2\)
по часовой стрелке
от \(\displaystyle AB \) до положения касания с нижней дугой | При повороте прямой \(\displaystyle y=a(x-5)+2\)
против часовой стрелки
от \(\displaystyle AB \) до положения касания с верхней дугой |
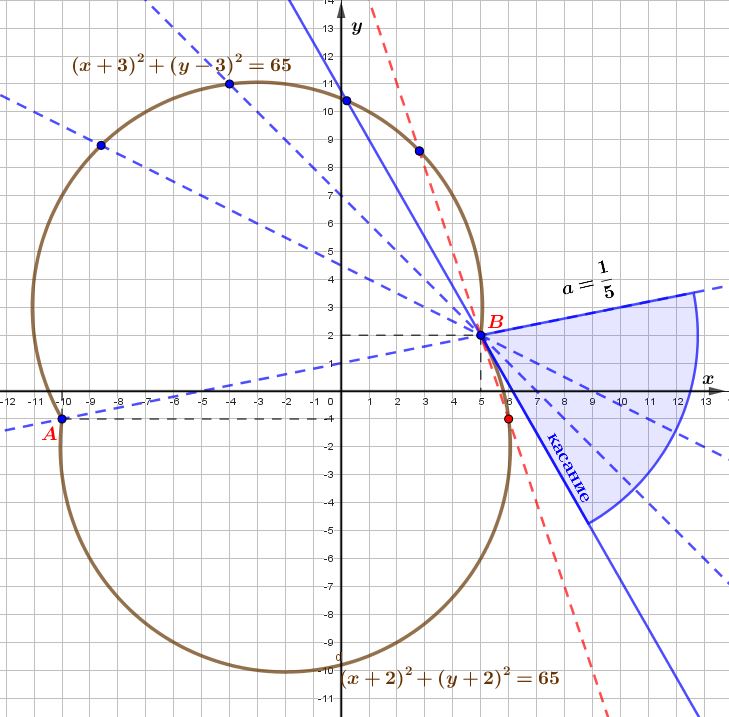 | 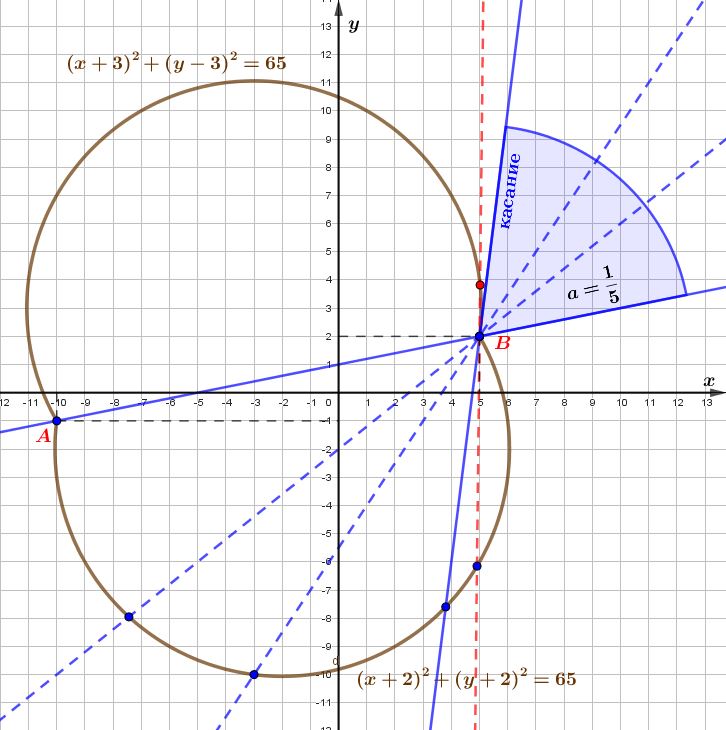 |
По рисункам видим, что в других случаях прямая \(\displaystyle y=a(x-5)+2\) имеет с графиком первого уравнения три точки пересечения (точка \(\displaystyle B\) и по одной точке с каждой из дуг).
Найдём значения \(\displaystyle a{\small ,}\) при которых прямая \(\displaystyle y=a(x-5)+2\) касается:
- нижней дуги,
- верхней дуги.
Прямая \(\displaystyle y =a(x-5)+2\)касается окружности \(\displaystyle (x+2)^2+(y+2)^2=65\) при \(\displaystyle a= -\frac{7}{4}{\small .}\)
Прямая \(\displaystyle y =a(x-5)+2\) касается окружности \(\displaystyle (x+2)^2+(y+2)^2=65\) в точке \(\displaystyle B(5;2){\small .}\)
По свойству касательной к окружности: касательная к окружности перпендикулярна радиусу, проведенному в точку касания. Значит, радиус \(\displaystyle C_{1}B\) перпендикулярен прямой \(\displaystyle y =a(x-5)+2{\small .}\)
ПравилоПризнак перпендикулярности прямыхПрямые \(\displaystyle y=k_{1}x+b_{1}\) и \(\displaystyle y=k_{2}x+b_{2}\) перпендикулярны, если \(\displaystyle k_{1} \cdot k_{2}=-1{\small .}\) | 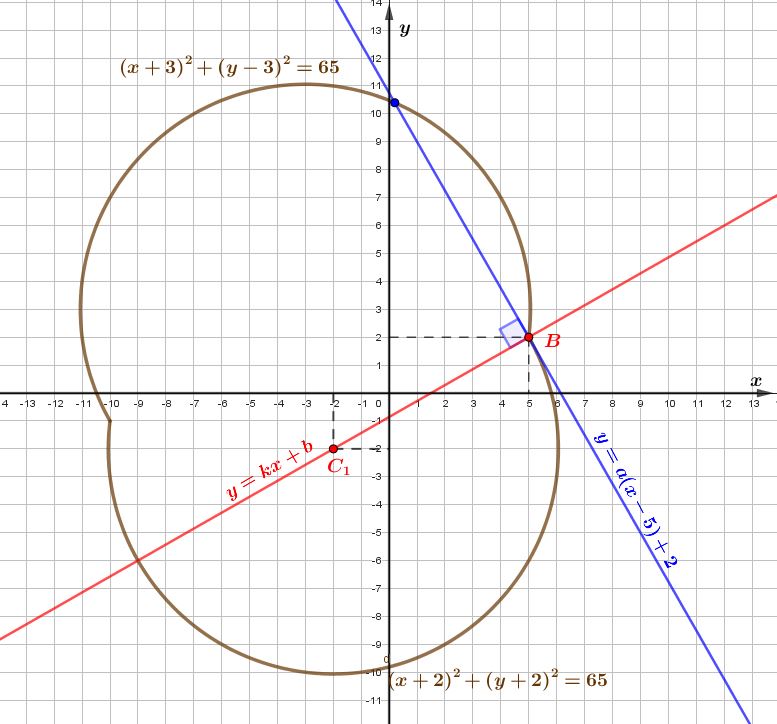 |
Найдем уравнение прямой \(\displaystyle C_{1}B{\small ,}\) перпендикулярной прямой \(\displaystyle y =a(x-5)+2{\small ,}\) в виде \(\displaystyle y=kx+b{\small .}\)
Точки \(\displaystyle C_{1}(\color{red}{-2};\color{red}{-2})\) и \(\displaystyle B(\color{blue}{5};\color{blue}{2})\) лежат на прямой, поэтому при подстановке их координат в уравнение прямой получим верные равенства:
\(\displaystyle \left\{\begin{aligned}\color{red}{-2} &=k \cdot (\color{red}{-2})+b{ \small ,}\\\color{blue}{2}&=k \cdot \color{blue}{5}+b{ \small .}\end{aligned}\right. \)
Вычитая из первого уравнения системы второе, получаем:
\(\displaystyle -4=-7k{ \small ,}\)
\(\displaystyle k= \frac {4}{7}{\small .}\)
Тогда \(\displaystyle a=- \frac{1}{k}=-\frac{7}{4}{\small .}\)
Таким образом, при \(\displaystyle a=-\frac{7}{4}\) прямая \(\displaystyle y =a(x-5)+2\) касается окружности \(\displaystyle (x+2)^2+(y+2)^2=65\) в точке \(\displaystyle B{\small .}\)
Прямая \(\displaystyle y =a(x-5)+2\) касается окружности \(\displaystyle (x+3)^2+(y-3)^2=65\) при \(\displaystyle a= 8{\small .}\)
Прямая \(\displaystyle y =a(x-5)+2\) касается окружности \(\displaystyle (x+3)^2+(y-3)^2=65\) в точке \(\displaystyle B(5;2){\small .}\)
Касательная к окружности перпендикулярна радиусу, проведенному в точку касания. Значит, радиус \(\displaystyle C_{2}B\) перпендикулярен прямой \(\displaystyle y =a(x-5)+2{\small .}\) Найдем уравнение прямой \(\displaystyle C_{2}B\) в виде \(\displaystyle y=kx+b{\small .}\) Для этого подставим в уравнение прямой точки \(\displaystyle C_{2}(\color{red}{-3};\color{red}{3})\) и \(\displaystyle B(\color{blue}{5};\color{blue}{2}){\small :}\) \(\displaystyle \left\{\begin{aligned} \color{red}{3} &=k \cdot (\color{red}{-3})+b{ \small ,}\\ \color{blue}{2}&=k \cdot \color{blue}{5}+b{ \small .} \end{aligned}\right. \) | 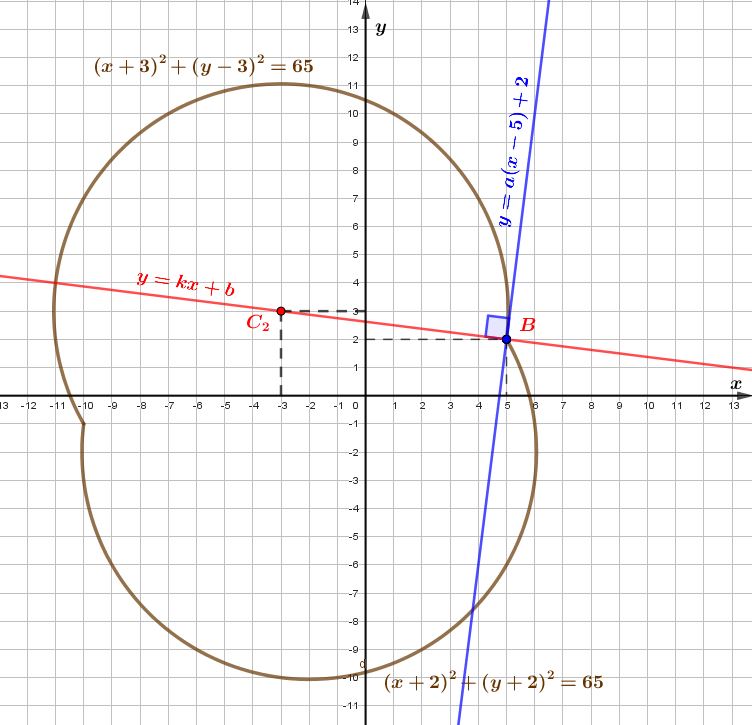 |
Вычитая из первого уравнения системы второе, получаем:
\(\displaystyle k=-\frac {1}{8}{\small .}\)
Тогда \(\displaystyle a=- \frac{1}{k}=8{\small .}\)
Значит, при \(\displaystyle a=8\) прямая \(\displaystyle y =a(x-5)+2\) касается окружности \(\displaystyle (x+3)^2+(y-3)^2=65\) в точке \(\displaystyle B{\small .}\)
Объединяя полученные результаты, видим, что при всех значениях \(\displaystyle a\) от \(\displaystyle -\frac {4}{7}\) до \(\displaystyle 8\) включительно прямая \(\displaystyle y =a(x-5)+2\) пересекает график первого уравнения исходной системы в двух точках.
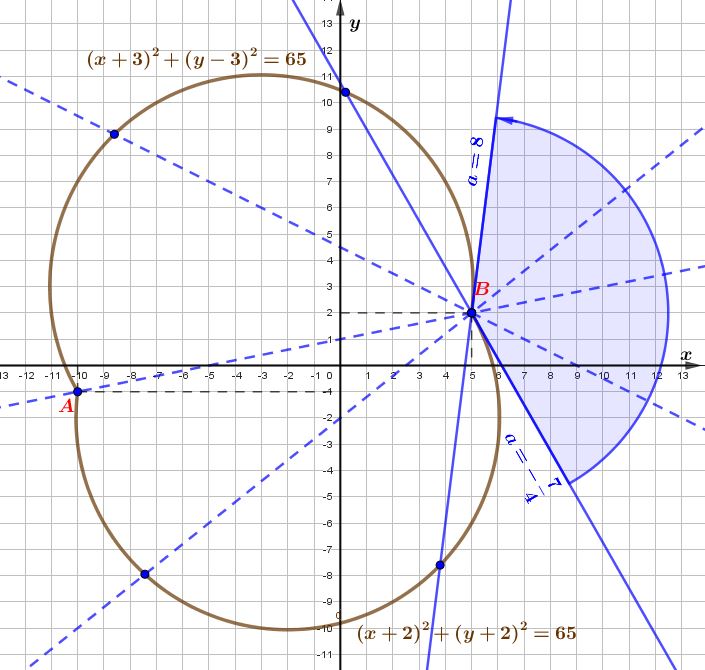
Значит, исходная система уравнений имеет ровно два решения при \(\displaystyle -\frac {7}{4} \leqslant a \leqslant 8 {\small .}\)
Ответ: \(\displaystyle -\frac {7}{4} \leqslant a \leqslant 8 {\small .}\)