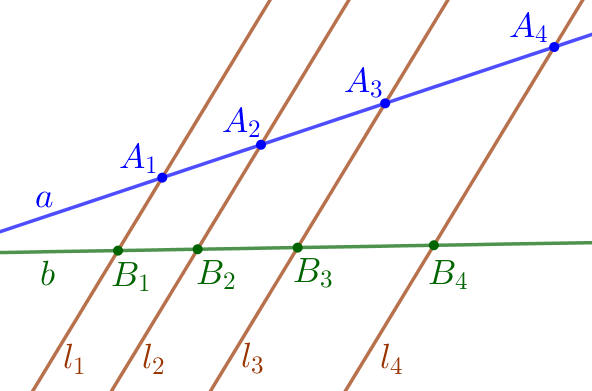
В треугольнике \(\displaystyle ABC\) медиана \(\displaystyle BE\) и биссектриса \(\displaystyle AD\) перпендикулярны и пересекаются в точке \(\displaystyle K{\small.}\) Найдите длину отрезка \(\displaystyle AK{\small,}\) если \(\displaystyle AD=12{\small.}\)
По условию задачи выполним чертёж.
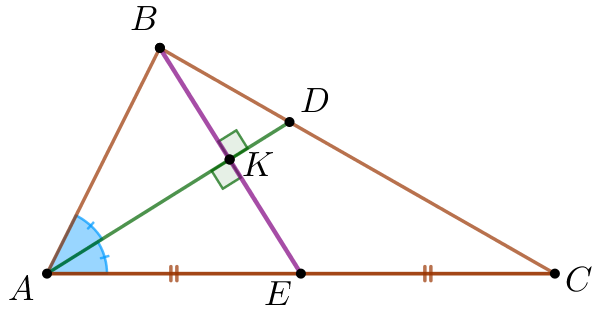 |
\(\displaystyle AE=EC {\small.}\)
\(\displaystyle \angle BAD=\angle CAD {\small.}\)
|
Требуется найти длину отрезка \(\displaystyle AK{\small.}\)
Пусть \(\displaystyle AK=x {\small,}\) тогда \(\displaystyle KD=12-x {\small.}\)
Выполним дополнительное построение.
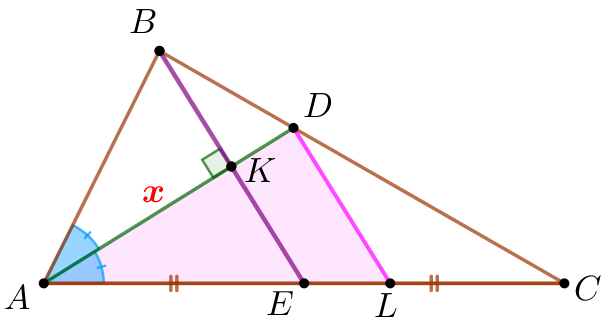 | Построим отрезок \(\displaystyle DL\) параллельно медиане \(\displaystyle BE{\small.}\) |
получаем:
\(\displaystyle \frac{AK}{KD}= \frac{AE}{EL} {\small;}\\ \)
\(\displaystyle \frac{x}{12-x}= \frac{AE}{EL} {\small.}\)
Пусть \(\displaystyle AE=EC=a {\small.}\) Тогда
\(\displaystyle \frac{x}{12-x}= \frac{a}{EL} {\small.}\)
Выразим \(\displaystyle EL\) через \(\displaystyle a {\small.}\)
Рассмотрим треугольник \(\displaystyle BCE{\small.}\)
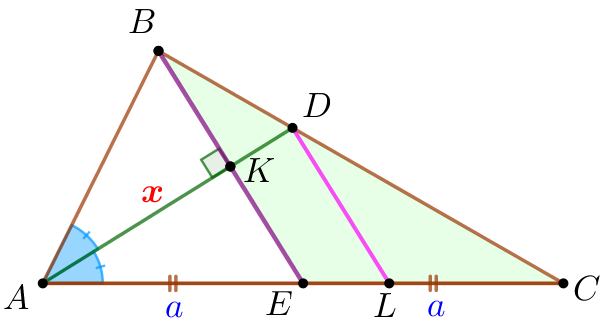 | По построению \(\displaystyle DL \parallel BE {\small.}\) По обобщённой теореме Фалеса получаем: \(\displaystyle \frac{EL}{LC}=\frac{BD}{DC}{\small.}\) |
По условию задачи \(\displaystyle AD\) – биссектриса треугольника \(\displaystyle ABC{\small.}\)
получаем:
\(\displaystyle \frac{BD}{DC}=\frac{AB}{AC}{\small.} \)
Значит,
\(\displaystyle \frac{EL}{LC}=\frac{AB}{AC}{\small.}\)
Рассмотрим треугольник \(\displaystyle ABE {\small.}\)
Так как биссектриса \(\displaystyle AK\) является и высотой треугольника \(\displaystyle ABE {\small,}\) то \(\displaystyle \triangle ABE \) – равнобедренный.
Следовательно, \(\displaystyle AB=AE=a {\small.}\) Поскольку \(\displaystyle AC=AE+EC \) и \(\displaystyle AE=EC=a {\small,}\) то \(\displaystyle AC=2 \cdot a{\small.}\) | 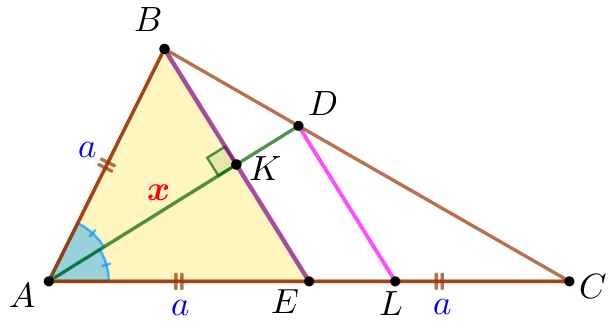 |
Получаем:
\(\displaystyle \frac{EL}{LC}=\frac{AB}{AC}= \frac{a}{2 \cdot a}=\frac{1}{2}{\small.}\\ \)
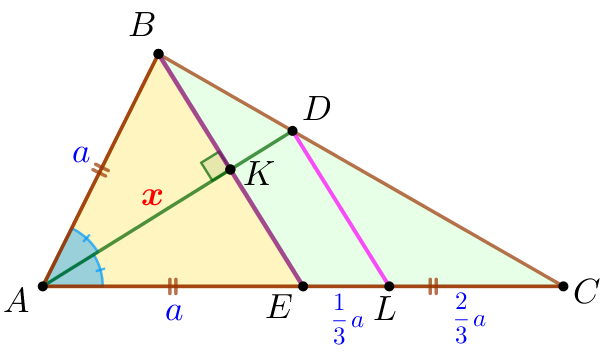 | То есть \(\displaystyle LC=2 \cdot EL {\small.}\) По рисунку \(\displaystyle EC=EL+LC {\small.}\) Тогда \(\displaystyle a=EL+ 2 \cdot EL=3 \cdot EL{\small.}\) Значит, \(\displaystyle EL= \frac{1}{3} \cdot a {\small.}\) |
Так как
\(\displaystyle \frac{x}{12-x}= \frac{a}{EL} \) и \(\displaystyle \frac{a}{EL}=\frac{\cancel{a}}{\frac{1}{3} \cdot \cancel{a}}=3 {\small,}\)
то
\(\displaystyle \frac{x}{12-x}= 3 {\small.}\)
Получаем
\(\displaystyle x=3 \cdot (12-x) {\small;}\)
\(\displaystyle x=36-3x {\small;}\)
\(\displaystyle 4 \cdot x=36 {\small;}\)
\(\displaystyle x=9 {\small.}\)
Значит, \(\displaystyle AK=9 {\small.}\)
Ответ: \(\displaystyle 9 {\small.}\)