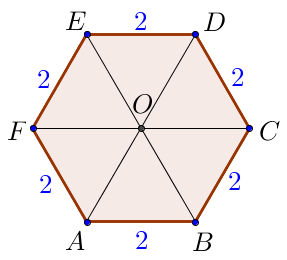
Найдите площадь \(\displaystyle S\) поверхности правильной шестиугольной призмы, если сторона её основания равна \(\displaystyle 2 \small, \) а боковое ребро \(\displaystyle 2\sqrt{3} \small. \) В ответ запишите \(\displaystyle \frac{S}{\sqrt{3}}\small. \)
Пусть \(\displaystyle ABCDEFA_1B_1C_1D_1E_1F_1\) – прямая призма, в основании которой лежит правильный шестиугольник \(\displaystyle ABCDEF \) со стороной\(\displaystyle AB=2 \small.\) Боковое ребро призмы \(\displaystyle AA_1=2\sqrt{3}\small. \) Высота прямой призмы равна её боковому ребру. Следовательно, высота призмы равна \(\displaystyle 2\sqrt{3}\small. \) |
Воспользуемся формулой для вычисления площади полной поверхности призмы.
Площадь полной поверхности призмы
Площадь полной поверхности призмы \(\displaystyle S \) равна
\(\displaystyle S=2 \cdot S_{осн}+S_{бок} { \small ,} \)
где \(\displaystyle S_{осн} \) – площадь основания,
\(\displaystyle S_{бок}\) – площадь боковой поверхности призмы.
Подставим найденные значения \(\displaystyle S_{осн}\) и \(\displaystyle S_{бок}\) в формулу площади полной поверхности призмы:
\(\displaystyle \begin{aligned}S&=2 \cdot S_{осн}+S_{бок} { \small ,} \\S&=2 \cdot 6\sqrt{3}+24 \sqrt{3}{ \small ,} \\S&=36 \sqrt{3}{ \small .} \\\end{aligned}\)
В ответ требуется записать \(\displaystyle \frac{S}{\sqrt{3}} \small: \)
\(\displaystyle \frac{S}{\sqrt{3}}= \frac{36 \sqrt{3}}{\sqrt{3}}=36\small. \)
Ответ: \(\displaystyle 36 \small. \)