Пожарную лестницу приставили к окну дома, которое расположено на высоте \(\displaystyle 12\)м от земли (см. рис.). Нижний конец лестницы отстоит от стены на \(\displaystyle 5\)м. Найдите длину лестницы. Ответ дайте в метрах.
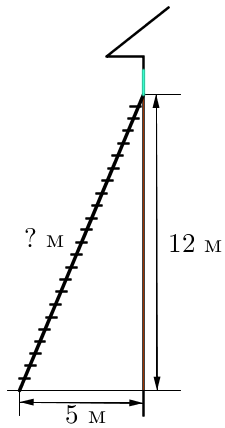
Пусть \(\displaystyle c\) – длина лестницы.
Изобразим предложенную в задаче конструкцию в виде прямоугольного треугольника \(\displaystyle ABC \small, \) в котором: \(\displaystyle \angle C =90^{\circ} \small, \) \(\displaystyle AB=c \small, \) \(\displaystyle AC=5 \small, \) \(\displaystyle BC=12 \small. \)
По теореме Пифагора \(\displaystyle AB^2=AC^2+BC^2 {\small,} \) \(\displaystyle c^2=5^2+12^2 {\small,} \) \(\displaystyle c^2=25+144=169 {\small,} \) \(\displaystyle c= \pm \sqrt{169}=\pm 13 \small. \) Так как \(\displaystyle c\) – длина гипотенузы \(\displaystyle AB \small, \) то \(\displaystyle c>0 \small. \) Значит, \(\displaystyle c=13 \small. \) | 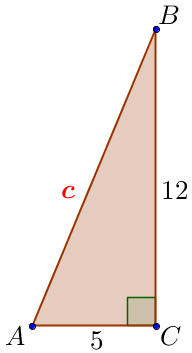 |
Длина лестницы равна \(\displaystyle 13\) метров.
Ответ: \(\displaystyle 13 \small. \)