Используя метод интервалов, решите неравенство
\(\displaystyle x^2-5x>-6{\small .}\)
\(\displaystyle x \in \)
Чтобы решить неравенство методом интервалов, преобразуем неравенство так, чтобы с одной стороны был ноль:
\(\displaystyle x^2-5x>-6{ \small ,}\)
\(\displaystyle x^2-5x+6>0{\small .}\)
Далее найдем все корни квадратного уравнения \(\displaystyle x^2-5x+6=0{\small .}\)
Отметим найденные корни на числовой прямой, выкалывая их (так как знак неравенства строгий):

Получаем три интервала:
\(\displaystyle (-\infty;2){ \small ,} \, (2;3)\) и \(\displaystyle (3;+\infty){\small .}\)
Определим знак функции \(\displaystyle f(x)=x^2-5x+6\) в каждом из данных интервалов.
Для интервала \(\displaystyle (-\infty;2)\) выберем \(\displaystyle x=0 \in (-\infty;2){\small .}\) Определим знак значения функции в точке \(\displaystyle x=0{ \small :}\)
\(\displaystyle f(0)=0^2-5\cdot 0+6>0{\small .}\)
Пишем знак плюс в интервале \(\displaystyle (-\infty;2){\small :}\)
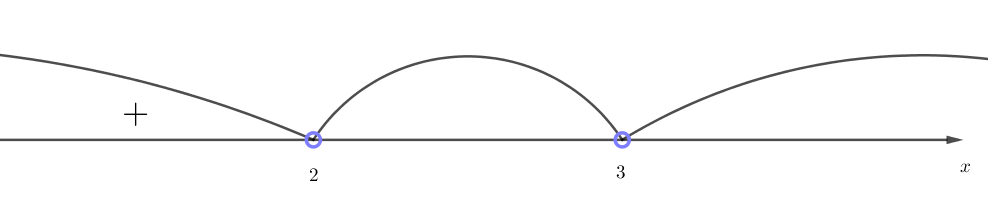
Для интервала \(\displaystyle (2;3)\) выберем \(\displaystyle x=2{,}5 \in (2;3){\small .}\) Определим знак значения функции в точке \(\displaystyle x=2{,}5 { \small :}\)
\(\displaystyle f(2{,}5)=2{,}5^2-5\cdot 2{,}5 +6=6{,}25-12{,}5+6<0{\small .}\)
Пишем знак минус в интервале \(\displaystyle (2;3){\small :}\)

Для интервала \(\displaystyle (3;+\infty)\) выберем \(\displaystyle x=4 \in (3;+\infty){\small .}\) Определим знак значения функции в точке \(\displaystyle x=4 { \small :}\)
\(\displaystyle f(4)=4^2-5\cdot 4 +6=16-20+6>0{\small .}\)
Пишем знак плюс в интервале \(\displaystyle (3;+\infty){\small :}\)

Так как решения неравенства \(\displaystyle x^2-5x+6>0\) соответствуют промежуткам, где функция \(\displaystyle f(x)=x^2-5x+6\) положительна, то
\(\displaystyle (-\infty;2) \cup(3;+\infty)\) – искомое решение.
Ответ: \(\displaystyle x \in (-\infty;2) \cup(3;+\infty){\small .}\)